
【題目】如圖![]() ,在平面直角坐標系中,二次函數
,在平面直角坐標系中,二次函數![]() 的圖象的頂點為
的圖象的頂點為![]() 點,與
點,與![]() 軸交于
軸交于![]() 點,與
點,與![]() 軸交于
軸交于![]() 、
、![]() 兩點,
兩點,![]() 點在原點的左側,
點在原點的左側,![]() 點的坐標為
點的坐標為![]() ,
,![]() ,
,![]() .
.
(![]() )求這個二次函數的表達式.
)求這個二次函數的表達式.
(![]() )經過
)經過![]() 、
、![]() 兩點的直線,與
兩點的直線,與![]() 軸交于點
軸交于點![]() ,在該拋物線上是否存在這樣的點
,在該拋物線上是否存在這樣的點![]() ,使以點
,使以點![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形為平行四邊形?若存在,請求出點
為頂點的四邊形為平行四邊形?若存在,請求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
(![]() )如圖
)如圖![]() ,若點
,若點![]() 是該拋物線上一點,點
是該拋物線上一點,點![]() 是直線
是直線![]() 下方的拋物線上一動點,當點
下方的拋物線上一動點,當點![]() 運動到什么位置時,
運動到什么位置時,![]() 的面積最大?求出此時
的面積最大?求出此時![]() 點的坐標和
點的坐標和![]() 的最大面積.
的最大面積.


【答案】(1) ![]() ;(2)存在點
;(2)存在點![]() ,坐標為
,坐標為![]() ;(3)
;(3)![]() ,
,![]() 最大為
最大為![]() .
.
【解析】
(1)求二次函數的表達式,需要求出A、B、C三點坐標.已知B點坐標,且OB=OC,可知C(0,3),![]() .則A坐標為(-1,0).將A,B,C三點坐標代入關系式,可求得二次函數的表達式.
.則A坐標為(-1,0).將A,B,C三點坐標代入關系式,可求得二次函數的表達式.
(2)已知拋物線關系式,求出頂點D坐標,求出直線CD,E是直線與x軸交點,可得E點坐標.四邊形AECF為平行四邊形,則![]() ,
,![]() ∥
∥![]() ,即可求出點F的坐標.
,即可求出點F的坐標.
(3)G在拋物線上,代入解析式求出G點坐標,過點![]() 作
作![]() 軸的平行線與
軸的平行線與![]() 交于點
交于點![]() ,設
,設![]() ,則
,則![]() ,可求出線段PQ的長度,
,可求出線段PQ的長度,![]() ,然后求當面積最大時x的值.
,然后求當面積最大時x的值.
(![]() )由已知得:
)由已知得:![]() ,
,![]() ,
,
將![]() ,
,![]() ,
,![]() 三點的坐標代入,得
三點的坐標代入,得 ,
,
∴![]() .
.
(![]() )存在.
)存在.
∵![]() ,
,
∴直線![]() 的解析式為:
的解析式為:![]() ,
,
∴![]() 點的坐標為
點的坐標為![]() ,
,
由![]() 、
、![]() 、
、![]() 、
、![]() 四點的坐標得:
四點的坐標得:![]() ,
,![]() ∥
∥![]() ,
,
∴以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點,的四邊形為平移四邊形,
為頂點,的四邊形為平移四邊形,
∴存在點![]() ,坐標為
,坐標為![]() .
.
(![]() )過點
)過點![]() 作
作![]() 軸的平行線與
軸的平行線與![]() 交于點
交于點![]() ,易得
,易得![]() ,直線
,直線![]() 為
為![]() ,
,
設![]() ,則
,則![]() ,
,
![]() ,
,![]() ,
,
當![]() 時,
時,![]() 最大,此時
最大,此時![]() ,
,![]() 最大為
最大為![]() .
.


科目:初中數學 來源: 題型:
【題目】拋物線y=x2﹣2x﹣15,y=4x﹣23,交于A、B點(A在B的左側),動點P從A點出發,先到達拋物線的對稱軸上的某點E再到達x軸上的某點F,最后運動到點B.若使點P動的總路徑最短,則點P運動的總路徑的長為( )
A. 10![]() B. 7
B. 7![]() C. 5
C. 5![]() D. 8
D. 8![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2019年5月26日第5屆中國國際大數據產業博覽會召開.某市在五屆數博會上的產業簽約金額的折線統計圖如圖.下列說法正確的是( )

A. 簽約金額逐年增加
B. 與上年相比,2019年的簽約金額的增長量最多
C. 簽約金額的年增長速度最快的是2016年
D. 2018年的簽約金額比2017年降低了22.98%
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】正方形ABCD的邊長為3,點E,F分別在射線DC,DA上運動,且DE=DF.連接BF,作EH⊥BF所在直線于點H,連接CH.
(1)如圖1,若點E是DC的中點,CH與AB之間的數量關系是 ;
(2)如圖2,當點E在DC邊上且不是DC的中點時,(1)中的結論是否成立?若成立給出證明;若不成立,說明理由;
(3)如圖3,當點E,F分別在射線DC,DA上運動時,連接DH,過點D作直線DH的垂線,交直線BF于點K,連接CK,請直接寫出線段CK長的最大值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠C=90°,BC=6,AC=4.點P、Q分別從點A、B同時出發,點P沿A→C的方向以每秒1個單位長的速度向點C運動,點Q沿B→C的方向以每秒2個單位長的速度向點C運動.當其中一個點先到達點C時,點P、Q停止運動.當四邊形ABQP的面積是△ABC面積的一半時,求點P運動的時間.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數![]() 的圖象與
的圖象與![]() 軸交于
軸交于![]() 、
、![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,點
,點![]() 的坐標為
的坐標為![]() ,且當
,且當![]() 和
和![]() 時二次函數的函數值
時二次函數的函數值![]() 相等.
相等.
(![]() )求實數
)求實數![]() 、
、![]() 的值.
的值.
(![]() )如圖
)如圖![]() ,動點
,動點![]() 、
、![]() 同時從
同時從![]() 點出發,其中點
點出發,其中點![]() 以每秒
以每秒![]() 個單位長度的速度沿
個單位長度的速度沿![]() 邊向終點
邊向終點![]() 運動,點
運動,點![]() 以每秒
以每秒![]() 個單位長度的速度沿射線
個單位長度的速度沿射線![]() 方向運動,當點
方向運動,當點![]() 停止運動時,點
停止運動時,點![]() 隨之停止運動.設運動時間為
隨之停止運動.設運動時間為![]() 秒.連接
秒.連接![]() ,將
,將![]() 沿
沿![]() 翻折,使點
翻折,使點![]() 落在點
落在點![]() 處,得到
處,得到![]() .
.
①是否存在某一時刻![]() ,使得
,使得![]() 為直角三角形?若存在,求出
為直角三角形?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
②設![]() 與
與![]() 重疊部分的面積為
重疊部分的面積為![]() ,求
,求![]() 關于
關于![]() 的函數關系式.
的函數關系式.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】等邊三角形![]() 的邊長為
的邊長為![]() ,將其放置在如圖所示的平面直角坐標系中,其中
,將其放置在如圖所示的平面直角坐標系中,其中![]() 邊在
邊在![]() 軸上,
軸上,![]() 邊的高
邊的高![]() 在
在![]() 軸上.一只電子蟲從
軸上.一只電子蟲從![]() 出發,先沿
出發,先沿![]() 軸到達
軸到達![]() 點,再沿
點,再沿![]() 到達
到達![]() 點,已知電子蟲在
點,已知電子蟲在![]() 軸上運動的速度是在
軸上運動的速度是在![]() 上運動速度的
上運動速度的![]() 倍,若電子蟲走完全程的時間最短,則點
倍,若電子蟲走完全程的時間最短,則點![]() 的坐標為________.
的坐標為________.

查看答案和解析>>
科目:初中數學 來源: 題型:
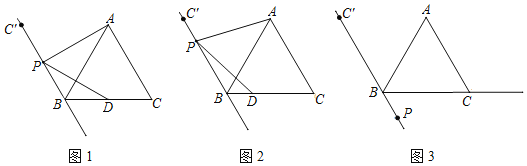
【題目】△ABC是等邊三角形,點C關于AB對稱的點為C′,點P是直線C′B上的一個動點,連接AP,作∠APD=60°交射線BC于點D.
(1)若點P在線段C′B上(不與點C′,點B重合)
①如圖1,當點P是線段C′B的中點時,直接寫出線段PD與線段PA的數量關系 .
②如圖2,點P是線段C′B上任意一點,證明PD與PA的數量關系.
(2)若點P在線段C′B的延長線上,
①依題意補全圖3;
②直接寫出線段BD,AB,BP之間的數量關系為: .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com