【題目】設一列數
中任意三個相鄰的數之和都是22，已知
，
，
，那么
=________．
【答案】5
【解析】
由任意三個相鄰數之和都是22，可知a1、a4、a7、…a3n+1相等，a2、a5、a8、…a3n+2相等，a3、a6、a9、…a3n相等，可以得出a19=a1=13，a66=a3=2x，根據
可求出x的值,再根據任意三個相鄰的數之和都是22,可求出相鄰的三個數的值,問題得以解決．
解：由任意三個相鄰數之和都是22可知：
a1+a2+a3=22，
a2+a3+a4=22，
a3+a4+a5=22，
…
an+an+1+an+2=22，
可以推出：a1=a4=a7=…=a3n+1，
a2=a5=a8=…=a3n+2，
a3=a6=a9=…=a3n，
所以a19=a1=13，a66=a3，
則2x=6-x，
解得x=2，
所以a2=22-4-13=5，
因此a2018=a2=5．
故答案為：5.
世紀百通期末金卷系列答案科目：初中數學 來源： 題型：
【題目】在一個不透明的盒子中放有四張分別寫有數字1、2、3、4的紅色卡片和三張分別寫有1、2、3的藍色卡片，卡片除顏色和數字外其它完全相同．
（1）從中任意抽取一張卡片，求該卡片上寫有數字1的概率；
（2）將3張藍色卡片取出后放入另外一個不透明的盒子內，然后在兩個盒子內各任意抽取一張卡片，以紅色卡片上的數字作為十位數，藍色卡片上的數字作為個位數組成一個兩位數，求這個兩位數不小于22的概率（請利用樹狀圖或列表法說明）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB=AC，點D、E在BC上，連接AD、AE，如果只添加一個條件使∠DAB=∠EAC，則添加的條件不能為（ ）
A. BD=CE B. AD=AE C. DA=DE D. BE=CD
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分線,AD=20,則BC的長是 ( )
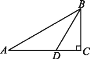
A. 20 B. 20
C. 30 D. 10
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，直線EF與MN相交于點O，∠MOE=30°，將一直角三角尺的直角頂點與點O重合，直角邊OA與MN重合，OB在∠NOE內部．操作：將三角尺繞點O以每秒5°的速度沿順時針方向旋轉一周，設運動時間為t（s）．
(1)當t為何值時，直角邊OB恰好平分∠NOE？此時OA是否平分∠MOE？請說明理由；
(2)若在三角尺轉動的同時，直線EF也繞點O以每秒8°的速度順時針方向旋轉一周，當一方先完成旋轉一周時，另一方同時停止轉動．
①當t為何值時，OE平分∠AOB？
②OE能否平分∠NOB？若能請直接寫出t的值；若不能，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】火車站、機場、郵局等場所都有為旅客提供打包服務的項目．現有一個長、寬、高分別為a、b 、30的箱子（其中a＞b），準備采用如圖①、②的兩種打包方式，所用打包帶的總長（不計接頭處的長）分別記為
．
（1）圖①中打包帶的總長
=________．
圖②中打包帶的總長
=________．
（2）試判斷哪一種打包方式更節省材料，并說明理由．（提醒：先判斷再說理，說理過程即為比較 的大小．）
（3）若b=40且a為正整數，在數軸上表示數的兩點之間有且只有19個整數點，求a 的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】隨著通訊技術的迅猛發展，人與人之間的溝通方式更多樣、便捷．某校數學興趣小組設計了“你最喜歡的溝通方式”調查問卷（每人必選且只選一種），在全校范圍內隨機調查了部分學生，將統計結果繪制了如下所示兩幅不完整的統計圖，請結合圖中所給信息，解答下列問題：
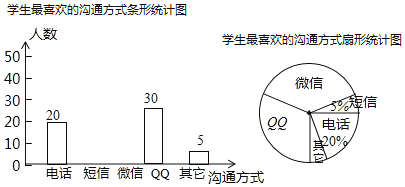
（1）本次調研活動共調研了多少名學生，表示“QQ”的扇形圓心角的度數是多少．
（2）請你補充完整條形統計圖；
（3）如果該校有2000名學生，請估計該校最喜歡用“微信”進行溝通的學生有多少名？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，方格紙中的每個小方格都是邊長為1個單位長度的正方形，建立平面直角坐標系，△ABC的頂點均在格點上．（不寫作法）
（1）以原點O為對稱中心，畫出△ABC關于原點O對稱的△A1B1C1，并寫出B1的坐標；
（2）再把△A1B1C1繞點C1 順時針旋轉90°，得到△A2B2C1，請你畫出△A2B2C1，并寫出B2的坐標．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com