
【題目】如圖,點A從坐標原點出發,沿x軸的正方向運動,點B坐標為(0,4),M是線段AB的中點,將點M繞點A順時針方向旋轉90°得到點C,過點C作x軸的垂線,垂足為F,過點B作y軸的垂線與直線CF相交于點E,連接AC,BC,設點A的橫坐標為t.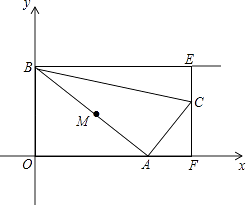
(1)當點C與點E恰好重合時,求t的值;
(2)當t為何值時,BC取得最小值;
(3)設△BCE的面積為S,當S=6時,求t的值.
【答案】
(1)解:當點C與點E重合時,如圖1,
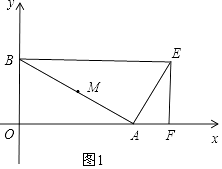
則OB=EF=4,OA=t,且AB=2AE,
∵由題意可知∠BAE=90°,
∴∠EAF+∠BAO=∠EAF+∠AEF=90°,
∴∠AEF=∠BAO,且∠EFA=∠AOB,
∴Rt△AEF∽Rt△BAO,
∴ ![]() =
= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得t=8
,解得t=8
(2)解:如圖2,
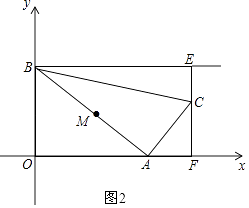
∵AB=2AC,
∴BC= ![]() =
= ![]() AC,
AC,
∴ ![]() ,
,
在Rt△AOB中,由勾股定理可得 ![]() ,
,
∴當t=0時,AB有最小,則BC有最小值
(3)解:①當0<t≤8時,則點C在點E的下方,如圖2,
同(1)可知 ![]() =
= ![]() =
= ![]() ,解得AF=2,CF=
,解得AF=2,CF= ![]() t,
t,
∴BE=OF=OA+AF=t+2,CE=EF﹣CF=4﹣ ![]() t,
t,
∴S= ![]() BECE=
BECE= ![]() (t+2)(4﹣
(t+2)(4﹣ ![]() t)=﹣
t)=﹣ ![]() t2+
t2+ ![]() t+4,
t+4,
令S=6,可得﹣ ![]() t2+
t2+ ![]() t+4=6,解得t=2或t=4;
t+4=6,解得t=2或t=4;
②當t>8時,則點C在點E的上方,如圖3,
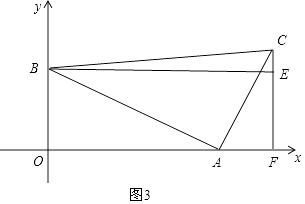
則CE=CF﹣EF= ![]() t﹣4,
t﹣4,
∴S= ![]() BECE=
BECE= ![]() (t+2)(
(t+2)( ![]() t﹣4)=
t﹣4)= ![]() t2﹣
t2﹣ ![]() t﹣4,
t﹣4,
令S=6可得 ![]() t2﹣
t2﹣ ![]() t﹣4=6,解得t=﹣4(舍去)或t=10,
t﹣4=6,解得t=﹣4(舍去)或t=10,
即當S的值為6時,t的值為2或4或10
【解析】(1)首先證明△AEF∽△BAO,然后依據相似三角形對應邊成比例的性質列方出求解即可;
(2)在Rt△ABC中可求得BC和AB的關系,然后在Rt△AOB中,用t可表示出AB,然后再可用t表示出BC,最后利用二次函數的性質可求得BC取得最小值時t的值;
(3)分為0<t≤8和t>8兩種情況求得S關于t的函數表達式,最后,再令S=6,從而可得到關于t的方程,從而可求得t的值.


科目:初中數學 來源: 題型:
【題目】甲、乙兩人參加某體育訓練項目,近期的五次測試成績得分情況如圖.
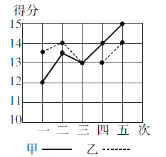
(1)分別求出兩人得分的平均數與方差;
(2)根據圖和上面算得的結果,對兩人的訓練成績作出評價.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于x的一元二次方程(m﹣2)2x2+(2m+1)x+1=0有兩個不相等的實數根,則m的取值范圍是( )
A.m< ![]()
B.m> ![]() 且m≠2
且m≠2
C.m≤ ![]()
D.m≥ ![]() 且m≠2
且m≠2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知數軸上點A表示的數為6,B是數軸上在A左側的一點,且A,B兩點間的距離為10.動點P從點A出發,以每秒5個單位長度的速度沿數軸向左勻速運動,動點Q從點B出發,以每秒3個單位長度的速度沿數軸向左勻速運動.(1)設運動時間為t(t>0)秒,數軸上點B表示的數是 ,點P表示的數是 (用含t的代數式表示);(2)若點P、Q同時出發,求:①當點P運動多少秒時,點P與點Q相遇?②當點P運動多少秒時,點P與點Q間的距離為8個單位長度?
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】讀句畫圖:如圖,直線CD與直線AB相交于C,
根據下列語句畫圖:

(1)過點P作PQ∥CD,交AB于點Q;
(2)過點P作PR⊥CD,垂足為R;
(3)若∠DCB=120°,猜想∠PQC是多少度?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在△ABC中,AB=AC. (1)若∠A=36,在△ABC中畫一條線段,能得到2個等腰三角形(不包括△ABC),這2個等腰三角形的頂角的度數分別是_____;(2)若∠A≠36, 當∠A=_____時,在等腰△ABC中畫一條線段,能得到2個等腰三角形(不包括△ABC).(寫出兩個答案即可)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com