
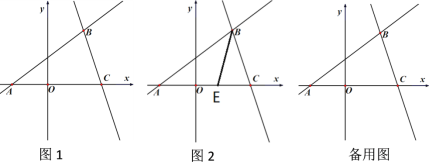
【題目】如圖1,在平面直角坐標系中,直線![]() :
:![]() 與
與![]() 軸交于點A,且經過點B(2,m),點C(3,0).
軸交于點A,且經過點B(2,m),點C(3,0).
(1)求直線BC的函數解析式;
(2)在線段BC上找一點D,使得△ABO與△ABD的面積相等,求出點D的坐標;
(3)y軸上有一動點P,直線BC上有一動點M,若△APM是以線段AM為斜邊的等腰直角三角形,求出點M的坐標;
(4)如圖2,E為線段AC上一點,連結BE,一動點F從點B出發,沿線段BE以每秒1個單位運動到點E,再沿線段EA以每秒![]() 個單位運動到A后停止,設點F在整個運動過程中所用時間為t,求t的最小值.
個單位運動到A后停止,設點F在整個運動過程中所用時間為t,求t的最小值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() ;(4) t最小值為
;(4) t最小值為![]() 秒
秒
【解析】
(1)把B(2,m)代入直線l解析式可求出m的值,即可得B點坐標,設直線BC的解析式為y=kx+b,把B、C兩點坐標代入可求得k、m的值,即可的直線BC的解析式;(2)過點O作![]() 交BC于點D,可知S△ABC=S△ABD,
交BC于點D,可知S△ABC=S△ABD,![]() ,聯立直線BC與OD的解析式解得交點D的坐標即可;(3)分別討論P點在y軸的負半軸和正半軸時兩種情況,①P點在y軸的負半軸時,作
,聯立直線BC與OD的解析式解得交點D的坐標即可;(3)分別討論P點在y軸的負半軸和正半軸時兩種情況,①P點在y軸的負半軸時,作![]() 于點N,可證明△AOP
于點N,可證明△AOP![]() △PNM1,設
△PNM1,設
OP=NM1=m,ON=m-2,則M1的坐標為(m,2-m),代入BC解析式即可求出m的值,進而可得M1坐標;②當P點在y軸正半軸時,同①解法可求出M2的坐標,綜上即可得答案;(4)作射線AQ與x軸正半軸的夾角為45°,過點B作x軸的垂線交射線AQ于點Q,作![]() 于點K,作
于點K,作![]() 于點T,可求出AG、AQ、BQ的長,根據時間t=
于點T,可求出AG、AQ、BQ的長,根據時間t=![]() +
+![]() =BE+EK≥BT,利用面積法求出BT的值即可.
=BE+EK≥BT,利用面積法求出BT的值即可.
(1)解:將點B(2,m)代入![]() 得m=3
得m=3
∴![]()
設直線BC解析式為![]() 得到
得到![]()
∴![]()
∴直線BC解析式為![]()
( 2 )如圖,過點O作![]() 交BC于點D
交BC于點D
∴S△ABC=S△ABD,![]()
∴直線OD的解析式為y=![]() x,
x,
∴
解得

![]()
(3)①如圖,當P點在y軸負半軸時,作![]() 于點N,
于點N,
∵直線AB與x軸相交于點A,
∴點A坐標為(-2,0),
∵∠APO+∠PAO=90°,∠APO+∠PNM1=90°
∴∠PAO=∠PNM1,
又∵AP=PM1,∠POA=∠PNM1=90°
∴△AOP![]() △PNM1,
△PNM1,
∴PN=OA=2,
設OP=NM1=m,ON=m-2
∴![]()
解得![]()
![]() ∴
∴![]()

②如圖,作![]() 于點H
于點H
可證明△AOP![]() △PHM2
△PHM2
設HM2=n,OH=n-2
∴![]()
解得![]()
∴M2(![]() ,
,![]() )
)

∴綜上所述![]() 或M2(
或M2(![]() ,
,![]() ).
).
(4)如圖,作射線AQ與x軸正半軸的夾角為45°,過點B作x軸的垂線交射線AQ于點Q,作![]() 于點K,作
于點K,作![]() 于點T,
于點T,
∵∠CAQ=45°BG⊥x軸,B(2,3)
∴AG=4,
∴AQ=4![]() ,BQ=7,
,BQ=7,
t=![]() =BE+EK≥BT,
=BE+EK≥BT,
由面積法可得:![]()
∴![]() ×4
×4![]() ×BT=
×BT=![]() ×7×4,
×7×4,
∴BT=![]()
因此t最小值為![]() .
.


 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案科目:初中數學 來源: 題型:
【題目】甲、乙兩組工人同時加工某種零件,乙組工作中有一次停產更換設備,更換設備
后,乙組的工作效率是原來的2倍.兩組各自加工零件的數量![]() (件)與時間
(件)與時間![]() (時)的函數圖
(時)的函數圖
象如圖所示.
(1)求甲組加工零件的數量y與時間![]() 之間的函數關系式.(2分)
之間的函數關系式.(2分)
(2)求乙組加工零件總量![]() 的值.(3分)
的值.(3分)
(3)甲、乙兩組加工出的零件合在一起裝箱,每夠300件裝一箱,零件裝箱的時間忽略不計,求經過多長時間恰好裝滿第1箱?再經過多長時間恰好裝滿第2箱?(5分)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:在數軸上A點表示數a,B點示數b,C點表示數c,b是最小的正整數,且a、c滿足|a+2|+(c-7)2=0.
![]()
(1)a=______,b=______,c=______;
(2)若將數軸折疊,使得A點與C點重合,則點B與數______表示的點重合;
(3)點A、B、C開始在數軸上運動,若點A以每秒1個單位長度的速度向左運動,同時,點B和點C分別以每秒2個單位長度和4個單位長度的速度向右運動,假設t秒鐘過后,若點A與點B之間的距離表示為AB,點A與點C之間的距離表示為AC,點B與點C之間的距離表示為BC.則AB=______,AC=______,BC=______.(用含t的代數式表示).
(4)直接寫出點B為AC中點時的t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC經過平移后得到△DEF,點A與點D,點B與點E,點C與點F分別是對應點,已知點A(3,3)、D(-2,1),解答下列問題:
(1)請在坐標系中畫出平移后的△DEF;
(2)請直接寫出以下點的坐標:B(___,___)、C(___,___)、E(___,___)、F(___,___);
(3)若點P(x,y)通過上述的平移規律平移得到的對應點為Q(3,5),則P點坐標為(____,____).

查看答案和解析>>
科目:初中數學 來源: 題型:
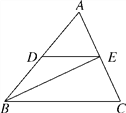
【題目】如圖,已知DE∥BC,BE平分∠ABC,∠C=65°,∠ABC=50°.
(1)求∠BED的度數;
(2)判斷BE與AC的位置關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△ABC中,∠A,∠B,∠C的對邊分別為a、b、c,下列說法中錯誤的是( )
A.如果∠C-∠B=∠A,則△ABC是直角三角形,且∠C=90;
B.如果![]() ,則△ABC是直角三角形,且∠C=90;
,則△ABC是直角三角形,且∠C=90;
C.如果(c+a)( c-a)=![]() ,則△ABC是直角三角形,且∠C=90;
,則△ABC是直角三角形,且∠C=90;
D.如果∠A:∠B:∠C=3:2:5,則△ABC是直角三角形,且∠C=90.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市文化宮學習十九大有關優先發展教育的精神,舉辦了為某貧困山區小學捐贈書包活動.首次用2000元在商店購進一批學生書包,活動進行后發現書包數量不夠,又購進第二批同樣的書包,所購數量是第一批數量的3倍,但單價貴了4元,結果第二批用了6300元.
(1)求文化官第一批購進書包的單價是多少?
(2)商店兩批書包每個的進價分別是68元和70元,這兩批書包全部售給文化宮后,商店共盈利多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC 中,AB=AC,∠B=50°,P 是邊 AB 上的一個動點(不與頂點 A 重合),則∠BPC 的度數可能是

A. 50° B. 80° C. 100° D. 130°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com