
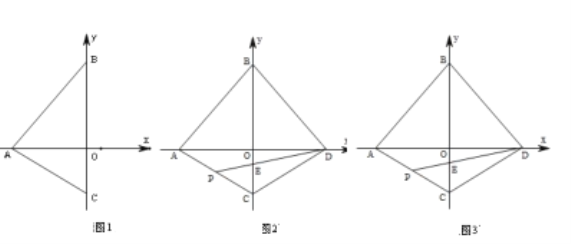
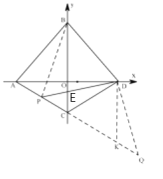
【題目】如圖,在平面直角坐標系中,點![]() 為坐標原點,直線
為坐標原點,直線![]() 與
與![]() 軸、
軸、![]() 軸分別交于點
軸分別交于點![]() 、
、![]() ,點
,點![]() 在
在![]() 軸負半軸上,且
軸負半軸上,且![]() .
.
(1)求![]() 的值;
的值;
(2)把![]() 沿
沿![]() 軸翻折,使點
軸翻折,使點![]() 落在
落在![]() 軸的點
軸的點![]() 處,點
處,點![]() 為線段
為線段![]() 上一點,連接
上一點,連接![]() 交
交![]() 軸于點
軸于點![]() ,設(shè)點
,設(shè)點![]() 橫坐標為
橫坐標為![]() ,
,![]() 的面積為
的面積為![]() ,求
,求![]() 與
與![]() 、
、![]() 的函數(shù)解析式(用含
的函數(shù)解析式(用含![]() 、
、![]() 的代數(shù)式表示);
的代數(shù)式表示);
(3)在(2)的條件下,若![]() ,點
,點![]() 的縱坐標為
的縱坐標為![]() ,求直線
,求直線![]() 的解析式.
的解析式.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)分別求出直線![]() 與x軸交點A,與y軸交點B的坐標,然后表示出OA,OC的長,從而求解;
與x軸交點A,與y軸交點B的坐標,然后表示出OA,OC的長,從而求解;
(2)過點![]() 作
作![]() 軸于
軸于![]() ,過點
,過點![]() 作
作![]() 于
于![]() ,由(1)可得∠ACB=60°,則∠OAC=30°,然后利用解直角三角形分別表示出PC,DN的長,從而求三角形面積,使問題得解;
,由(1)可得∠ACB=60°,則∠OAC=30°,然后利用解直角三角形分別表示出PC,DN的長,從而求三角形面積,使問題得解;
(3)連接![]() ,延長
,延長![]() 至
至![]() ,使得
,使得![]() ,過點
,過點![]() 作
作![]() ∥y軸交
∥y軸交![]() 于
于![]() ,通過對
,通過對![]() ,
,![]() 的判定得到
的判定得到![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,然后利用平行線分線段成比例定理求得m的值,從而確定點D和點E的坐標,然后利用待定系數(shù)法求函數(shù)解析式.
,然后利用平行線分線段成比例定理求得m的值,從而確定點D和點E的坐標,然后利用待定系數(shù)法求函數(shù)解析式.
解:(1)在![]() 中,當y=0時,x=
中,當y=0時,x=![]() ;當x=0時,y=6m
;當x=0時,y=6m
∴點![]() 坐標
坐標![]() ,點
,點![]() 坐標
坐標![]()
∴![]() ,
,![]() ,
,![]()
在![]() 中,
中,![]()
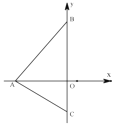
(2)過點![]() 作
作![]() 軸于
軸于![]() ,過點
,過點![]() 作
作![]() 于
于![]() .
.
∵點![]() 橫坐標為
橫坐標為![]()
∴![]() ,
,
由![]() ,則∠ACB=60°
,則∠ACB=60°
∴∠OAC=30°
∵PH∥OA
∴![]()
∴![]() ,
,
∴![]() ,解得:
,解得:![]()
在![]() 中,
中,![]()
∴![]()
∴![]()
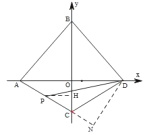
(3)連接![]() ,延長
,延長![]() 至
至![]() ,使得
,使得![]() ,過點
,過點![]() 作
作![]() ∥y軸交
∥y軸交![]() 于
于![]() .
.
由折疊性質(zhì)可知:∠ACB=∠DCB=60°,
∴∠QCD=60°
又因為CB=CQ,CD=CD
∴![]()
∴![]() ,
,![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]() 為等邊三角形
為等邊三角形
∵![]() ∥y軸
∥y軸
∴∠BCD=∠DCQ=∠CDK=60°
∴![]() 為等邊三角形
為等邊三角形
∴![]()
∴![]()
∴![]()
∴![]()
∵點![]() 縱坐標為
縱坐標為![]()
∴![]() ,
,![]()
∵CE∥DK
∴![]() ,即
,即![]()
解得:![]()
∴直線AB的解析式為![]()
當y=0時,![]() ,解得
,解得![]()
則A坐標為![]()
∴由折疊性質(zhì)可知,![]() 坐標為
坐標為![]() ,點
,點![]() 坐標為
坐標為![]()
設(shè)![]() 解析式為
解析式為![]() ,則
,則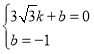 ,解得
,解得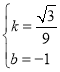
∴直線![]() 解析式為
解析式為![]() .
.


科目:初中數(shù)學 來源: 題型:
【題目】解不等式組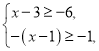
![]() 請結(jié)合題意填空,完成本題的解答.
請結(jié)合題意填空,完成本題的解答.
(Ⅰ)解不等式①,得_______________;
(Ⅱ)解不等式②,得_______________;
(Ⅲ)把不等式①和②的解集在數(shù)軸上表示出來;
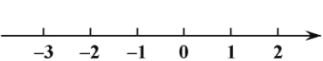
(Ⅳ)原不等式組的解集為____________.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,以AB為直徑的⊙O分別交AC、BC于點D、E,點F在AC的延長線上,且∠CBF=![]() ∠CAB.
∠CAB.
(1)求證:直線BF是⊙O的切線;
(2)若AB=5,sin∠BAD=![]() ,求AD的長;
,求AD的長;
(3)試探究FB、FD、FA之間的關(guān)系,并證明.
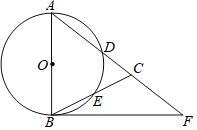
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AD∥BC,BA=BC,BD平分∠ABC.
(1)求證:四邊形ABCD是菱形;
(2)過點D作DE⊥BD,交BC的延長線于點E,若BC=5,BD=8,求四邊形ABED的周長.
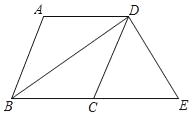
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】![]() 年我國個人所得稅征收辦法最新規(guī)定:月收入不超過
年我國個人所得稅征收辦法最新規(guī)定:月收入不超過![]() 元的部分不收稅;月收入超過
元的部分不收稅;月收入超過![]() 元但不超過
元但不超過![]() 元的部分征收
元的部分征收![]() 的所得稅;月收入超過
的所得稅;月收入超過![]() 元但不超過
元但不超過![]() 元的部分征收
元的部分征收![]() 的所得稅
的所得稅![]() 國家特別規(guī)定月收入指個人工資收入扣除專項附加費后的實際收入(專項附加費就是子女教育費用、住房貸款利息費用、租房的租金、贍養(yǎng)老人、大病醫(yī)療費用等費用).如某人月工資收入
國家特別規(guī)定月收入指個人工資收入扣除專項附加費后的實際收入(專項附加費就是子女教育費用、住房貸款利息費用、租房的租金、贍養(yǎng)老人、大病醫(yī)療費用等費用).如某人月工資收入![]() 元,專項附加費支出
元,專項附加費支出![]() 元,他應繳納個人所得稅為:
元,他應繳納個人所得稅為:![]() (元).
(元).
(1)當月收入超過![]() 元而又不超過
元而又不超過![]() 元時,寫出應繳納個人所得稅
元時,寫出應繳納個人所得稅![]() (元)與月收入
(元)與月收入![]() (元)之間的關(guān)系式;
(元)之間的關(guān)系式;
(2)如果某人當月專項附加費支出![]() 元,繳納個人所得稅
元,繳納個人所得稅![]() 元,那么此人本月工資是多少元?
元,那么此人本月工資是多少元?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖所示,在銳角三角形ABC中,AB=8,AC=5,BC=6,沿過點B的直線折疊這個三角形,使點C落在AB邊上的點E處,折痕為BD,下列結(jié)論:①∠CBD=∠EBD,②DE⊥AB,③三角形ADE的周長是7,④![]() ,⑤
,⑤![]() .其中正確的個數(shù)有( )
.其中正確的個數(shù)有( )
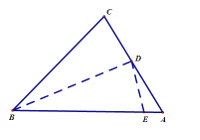
A.2B.3C.4D.5
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在每個小正方形的邊長為1的網(wǎng)格中,點![]() ,
,![]() ,
,![]() ,
,![]() 均在格點上,點
均在格點上,點![]() 是在直線
是在直線![]() 上的動點,連
上的動點,連![]() ,點
,點![]() 是點
是點![]() 關(guān)于直線
關(guān)于直線![]() 的對稱點.
的對稱點.
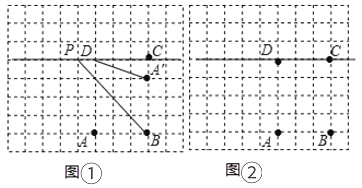
(1)在圖①中,當![]() (點
(點![]() 在點
在點![]() 的左側(cè))時,計算
的左側(cè))時,計算![]() 的值等于______.
的值等于______.
(2)當![]() 取得最小值時,請在如圖②所示的網(wǎng)格中,用無刻度的直尺畫出點
取得最小值時,請在如圖②所示的網(wǎng)格中,用無刻度的直尺畫出點![]() ,并簡要說明點
,并簡要說明點![]() 的位置是如何找到的.(不要求證明)
的位置是如何找到的.(不要求證明)
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】將矩形紙片OABC放在平面直角坐標系中,0為坐標原點,點A在y軸上,點C在x軸上,點B的坐標是(8,6),點P是邊AB上的一個動點,將△OAP沿OP折疊,使點A落在點Q處.
(1)如圖①,當點Q恰好落在OB上時.求點p的坐標;
(2)如圖②,當點P是AB中點時,直線OQ交BC于M點.
①求證:MB=MQ;②求點Q的坐標.

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com