
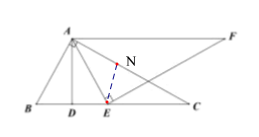
【題目】如圖,在![]() 中,
中,![]() .
.![]() 于
于![]() .
.![]() 為邊
為邊![]() 上的一個(不與
上的一個(不與![]() 、
、![]() 重合)點,且
重合)點,且![]() 于
于![]() 相交于點
相交于點![]() .
.

(1)填空:![]() ______;
______;![]() ______.
______.
(2)當![]() 時,證明:
時,證明:![]() .
.
(3)![]() 面積的最小值是_______.
面積的最小值是_______.
(4)當![]() 的內心在
的內心在![]() 的外部時,直接寫出
的外部時,直接寫出![]() 的范圍______.
的范圍______.
【答案】(1)![]() ;(2)見解析;(3)
;(2)見解析;(3)![]() ;(4)
;(4)![]() .
.
【解析】
(1)根據銳角三角函數的定義以及三角形內角和定理,即可求解;
(2)由ASA,即可證明![]() ;
;
(3)由題意得:![]() 面積=
面積=![]() AE2,當AE⊥BC時,AE=
AE2,當AE⊥BC時,AE=![]() ,進而即可求解;
,進而即可求解;
(4)當![]() 的內心恰好落在AC上時,設
的內心恰好落在AC上時,設![]() 的內心為N,易證
的內心為N,易證![]() 是等邊三角形,此時,AE=2,進而即可得到結論.
是等邊三角形,此時,AE=2,進而即可得到結論.
(1)∵在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() 180°-90°-60°=30°.
180°-90°-60°=30°.
故答案是:![]() ;
;
(2)![]() 于
于![]() ,
,
![]() ,
,
又∵![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
又∵![]() ,
,
![]() ;
;
(3)∵![]() =60°,
=60°,
∴EF=![]() AE,
AE,
∴![]() 面積=
面積= ![]() EFAE=
EFAE=![]() AE2,
AE2,
∴當AE的長最小時,![]() 面積的最小,即:AE⊥BC時,
面積的最小,即:AE⊥BC時,![]() 面積的最小.
面積的最小.
∴AE的最小值=ABsin60°=2×![]() =
=![]() ,此時,
,此時,![]() 面積的最小值=
面積的最小值=![]() .
.
故答案是:![]() .
.
(4)當![]() 的內心恰好落在AC上時,設
的內心恰好落在AC上時,設![]() 的內心為N,連接EN,
的內心為N,連接EN,
∵N是![]() 的內心,
的內心,
∴AN平分∠EAF,EN平分∠AEF,
∴∠EAC=![]() ∠EAF=30°,
∠EAF=30°,
∵∠BAC=90°,
∴∠BAE=∠BAC-∠EAC=90°-30°=60°,
又∵∠B=60°,
∴![]() 是等邊三角形,
是等邊三角形,
∴AE=AB=2,
∵![]() 為邊
為邊![]() 上的一個(不與
上的一個(不與![]() 、
、![]() 重合)點,由(1)可知
重合)點,由(1)可知![]() ,
,
∴當![]() 的內心在
的內心在![]() 的外部時,
的外部時,![]() .
.
故答案是:![]() .
.


科目:初中數學 來源: 題型:
【題目】已知二次函數y=﹣x2+x+6及一次函數y=﹣x+m,將該二次函數在x軸上方的圖象沿x軸翻折到x軸下方,圖象的其余部分不變,得到一個新函數(如圖所示),請你在圖中畫出這個新圖象,當直線y=﹣x+m與新圖象有4個交點時,m的取值范圍是( )

A. ﹣![]() <m<3 B. ﹣
<m<3 B. ﹣![]() <m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
<m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,A,B兩地被池塘隔開,小明通過下列方法測出了A、B間的距離:先在AB外選一點C,然后測出AC,BC的中點M,N,并測量出MN的長為12m,由此他就知道了A、B間的距離.有關他這次探究活動的描述錯誤的是( )

A. AB=24m B. MN∥AB
C. △CMN∽△CAB D. CM:MA=1:2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】金松科技生態農業養殖有限公司種植和銷售一種綠色羊肚菌,已知該羊肚菌的成本是12元/千克,規定銷售價格不低于成本,又不高于成本的兩倍.經過市場調查發現,某天該羊肚菌的銷售量y(千克)與銷售價格x(元/千克)的函數關系如下圖所示:

(1)求y與x之間的函數解析式;
(2)求這一天銷售羊肚菌獲得的利潤W的最大值;
(3)若該公司按每銷售一千克提取1元用于捐資助學,且保證每天的銷售利潤不低于3600元,問該羊肚菌銷售價格該如何確定.
查看答案和解析>>
科目:初中數學 來源: 題型:
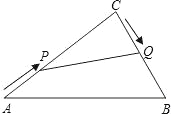
【題目】在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm.現有動點P從點A出發,沿AC向點C方向運動,動點Q從點C出發,沿線段CB也向點B方向運動.如果點P的速度是4cm/秒,點Q的速度是2cm/秒,它們同時出發,當有一點到達所在線段的端點時,就停止運動,設運動的時間為t秒.
(1)用含t的代數式表示Rt△CPQ的面積S;
(2)當t=3秒時,P、Q兩點之間的距離是多少?
(3)當t為多少秒時,以點C、P、Q為頂點的三角形與△ABC相似?
查看答案和解析>>
科目:初中數學 來源: 題型:
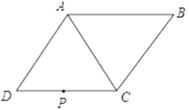
【題目】如圖,在菱形ABCD中,∠ADC=60°,CD=4![]() cm,P為CD的中點.
cm,P為CD的中點.
(1)在AC上找一點Q,使DQ+PQ的值最小(保留畫圖痕跡,不寫畫法,不必說理);
(2)求出(1)中DQ+PQ的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
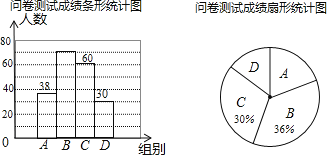
【題目】為了了解同學們對垃圾分類知識的了解程度,增強同學們的環保意識某校數學興趣小組設計了“垃圾分類知識及投放情況”問卷,并在本校隨機抽取若干名同學進行了問卷測試,根據測試成績分布情況,將測試成績分成A、B、C、D四組,繪制了如下統計圖表
問卷測試成績分組表
組別 | 分數/分 |
A | 60<x≤70 |
B | 70<x≤80 |
C | 80<x≤90 |
D | 90<x≤100 |
(1)本次抽樣調查的樣本總量是 ;
(2)樣本中,測試成績在B組的頻數是 ,D組的頻率是 ;
(3)樣本中,這次測試成績的中位數落在 組;
(4)如果該校共有880名學生,請估計成績在90<x≤100的學生約有 人.
查看答案和解析>>
科目:初中數學 來源: 題型:
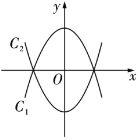
【題目】如圖,已知拋物線![]() ,將拋物線
,將拋物線![]() 沿
沿![]() 軸翻折,得到拋物線
軸翻折,得到拋物線![]() .
.
(1)求出拋物線![]() 的函數表達式;
的函數表達式;
(2)現將拋物線![]() 向左平移
向左平移![]() 個單位長度,平移后得到的新拋物線的頂點為
個單位長度,平移后得到的新拋物線的頂點為![]() ,與
,與![]() 軸的交點從左到右依次為
軸的交點從左到右依次為![]() ,
,![]() ;將拋物線
;將拋物線![]() 向右也平移
向右也平移![]() 個單位長度,平移后得到的新拋物線的頂點為
個單位長度,平移后得到的新拋物線的頂點為![]() ,與
,與![]() 軸交點從左到右依次為
軸交點從左到右依次為![]() ,
,![]() .在平移過程中,是否存在以點
.在平移過程中,是否存在以點![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形是矩形的情形?若存在,請求出此時
為頂點的四邊形是矩形的情形?若存在,請求出此時![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com