【題目】如圖，反比例函數圖象在第一象限的分支上有一點C（1，3），過點C的直線y = kx+b〔k< 0〕與x軸交于點A.
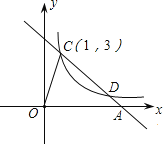
（1）求反比例函數的解析式；
（2）當直線與反比例函數的圖象在第一象限內的另一交點的橫坐標為3時，求△COD的面積.
【答案】（1）
；（2）4.
【解析】
（1）∵點C（1，3）在反比例函數圖象上，∴k1=1×3=3可求反比例函數的解析式；
（2）由直線與反比例函數的圖象在第一象限內的另一交點的橫坐標為3，易求其解析式，進而求出直線與x軸交點坐標，即可求出△COD的面積．
（1）∵點C（1，3）在反比例函數圖象上，
∴k=1×3=3，
∴y＝
；
（2）當x=3時，y=
=1，
∴D（3，1）．
∵C（1，3）、D（3，1）在直線y=k2x+b上，
∴
，
∴
．
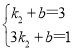∴y=-x+4．
令y=0，則x=4，
∴A（4，0），
∴S△COA=
×4×3=6，
S△DOA=×4×1=2，
∴△COD的面積=S△COA-S△DOA=6-2=4．
閱讀快車系列答案科目：初中數學 來源： 題型：
【題目】如圖，點E是矩形ABCD中CD邊上一點，△BCE沿BE折疊為△BFE，點F落在AD上．
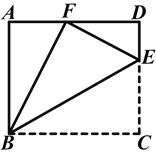
（1）求證：△ABF∽△DFE；
（2）若
，求tan∠EBC的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
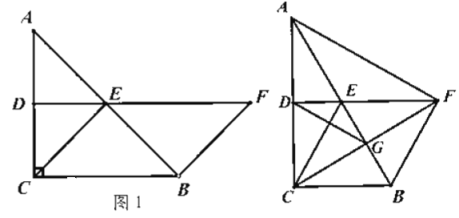
【題目】如圖1，
中，
，
是
的中點，
平分
交
于點
，
在
的延長線上且
．
（1）求證：四邊形
是平行四邊形；
（2）如圖2若四邊形是菱形，連接
，
，與交于點
，連接
，在不添加任何輔助線的情況下，請直接寫出圖2中的所有等邊三角形．
查看答案和解析>>
科目：初中數學 來源： 題型：
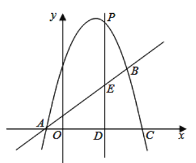
【題目】如圖，拋物線
與直線
相交于
，
兩點，且拋物線經過點
（1）求拋物線的解析式．
（2）點
是拋物線上的一個動點（不與點
點
重合），過點作直線
軸于點
，交直線
于點
．當
時，求點坐標；
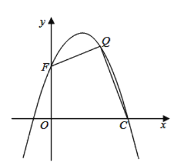
（3）如圖所示，設拋物線與
軸交于點
，在拋物線的第一象限內，是否存在一點
，使得四邊形
的面積最大？若存在，請求出點的坐標；若不存在，說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
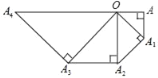
【題目】如圖，在等腰Rt△OAA1中，∠OAA1＝90°，OA＝1，以OA1為直角邊作等腰Rt△OA1A2，以OA2為直角邊作等腰Rt△OA2A3，…則OA8的長度為_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，平行四邊形ABCD中，對角線AC、BD相交于點O，E、F是AC上的兩點，當E、F滿足下列哪個條件時，四邊形DEBF不一定是平行四邊形（ ）
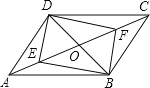
A.∠ADE=∠CBFB.∠ABE=∠CDFC.DE=BFD.OE=OF
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知直線l切⊙O于點A，B為⊙O上一點，過點B作BC⊥l，垂足為點C，連接AB、OB．
（1）求證：∠ABC＝∠ABO；
（2）若AB＝
，AC＝1，求⊙O的半徑．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
