
如圖所示的直線AE與四邊形ABCD的外接圓相切于A點.若∠DAE=12°,![]() 、
、![]() 、
、![]() 三弧的度數相等,則∠ABC的度數為何?( )
三弧的度數相等,則∠ABC的度數為何?( )

|
| A. | 64 | B. | 65 | C. | 67 | D. | 68 |
考點:
切線的性質。
專題:
計算題。
分析:
作直徑AF,連接DF,根據切線的性質求出∠F的度數,求出弧AD的度數,求出DC的度數,得出弧ADC的度數,即可求出答案.
解答:
解:作直徑AF,連接DF,
∵AE是⊙O的切線,
∴∠EAF=90°,
∵∠ADF=90°,
∴∠EAD+∠DAF=90°,∠F+∠DAF=90°,
∴∠F=∠DAE
∵∠DAE=12°(已知),
∴∠F=12°,
∴弧AD的度數是2×12°=24°,
∴![]() 、
、![]() 、
、![]() 三弧的度數相等,
三弧的度數相等,
∴弧CD的度數是![]() ×(360°﹣24°)=112°,
×(360°﹣24°)=112°,
∴弧ADC的度數是24°+112°=136°,
∴∠ABC=![]() ×136°=68°,
×136°=68°,
故選D.

點評:
本題考查了切線的性質的應用,能求出弧AD的度數是解此題的關鍵,弦切角等于該弦所夾弧所對的圓周角,主要培養學生運用性質進行推理和計算的能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
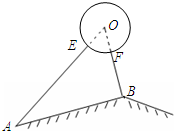 安裝在屋頂的太陽能熱水器的橫截面示意圖如圖所示.集熱管AE與支架BF所在直線相交于水箱橫截面⊙O的圓心O處,⊙O的半徑為0.2m,AO與屋面AB的夾角為32°,BF⊥AB于B,AB=2m,求支架BF的長(精確到0.1m).參考數據:sin32°=0.32,cos32°=0.84,tan32°=0.62.
安裝在屋頂的太陽能熱水器的橫截面示意圖如圖所示.集熱管AE與支架BF所在直線相交于水箱橫截面⊙O的圓心O處,⊙O的半徑為0.2m,AO與屋面AB的夾角為32°,BF⊥AB于B,AB=2m,求支架BF的長(精確到0.1m).參考數據:sin32°=0.32,cos32°=0.84,tan32°=0.62.查看答案和解析>>
科目:初中數學 來源: 題型:
 (2012•臺灣)如圖所示的直線AE與四邊形ABCD的外接圓相切于A點.若∠DAE=12°,
(2012•臺灣)如圖所示的直線AE與四邊形ABCD的外接圓相切于A點.若∠DAE=12°, |
| AB |
 |
| BC |
 |
| CD |
查看答案和解析>>
科目:初中數學 來源: 題型:單選題
 如圖所示的直線AE與四邊形ABCD的外接圓相切于A點.若∠DAE=12°,
如圖所示的直線AE與四邊形ABCD的外接圓相切于A點.若∠DAE=12°, 、
、 、
、 三弧的度數相等,則∠ABC的度數為何?
三弧的度數相等,則∠ABC的度數為何?查看答案和解析>>
科目:初中數學 來源:2012年臺灣省中考數學試卷(解析版) 題型:選擇題
 、
、 、
、 三弧的度數相等,則∠ABC的度數為何?( )
三弧的度數相等,則∠ABC的度數為何?( )
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com