
求證:(1)∠APD=∠BPD ;
(2)PA·PB=PC2+AC·CB.
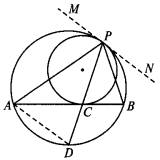
| (1)過點P作兩圓的公切線MN.
∵ MN與AB均為小圓的公切線,∴ ∠NPC=∠BCP. ∵ ∠NPC=∠NPB+∠BPC,∠BCP=∠PAC+∠APC, 又∠NPB=∠PAB=∠PAC,∴ ∠NPB+∠BPC=∠PAC+∠APC. ∴ ∠BPC=∠APC,即∠BPD =∠APD. (2)連結AD.由(1)知,∠DPA=∠BPC, 又∵ ∠ADP=∠CBP,∴ △PDA∽△PBC, ∴ 即PA·PB=PC·PD. ∵ PA·PB=PC·PD=(PC+CD)·PC=PC2+CD·PC, 又PC·CD=AC·BC,∴ PA·PB=PC2+AC·BC.
|
| (1)因為∠PAC+∠APC=∠PCB=∠NPB+∠CPB,所以只要證明∠PAC=∠NPB即可.
(2)要證明PA·PB=PC2+AC·CB,根據相交弦定理,得AC·BC=PC·CD,即證PA·PB=PC2+PC·CD=PC(PC+CD)=PC·PD.只需證△PDA∽△PBC即可. 兩圓相切時,常作公切線(內切時,常作外公切線;外切時,常作內公切線),兩圓的公切線使兩圓有公共的弦切角或相等的弦切角,從而把兩個圓中的角聯系起來.
|


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
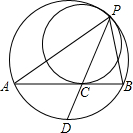 已知;如圖,兩圓內切于點P,大圓的弦AB切小圓于點C,PC的延長線交大圓于點D.
已知;如圖,兩圓內切于點P,大圓的弦AB切小圓于點C,PC的延長線交大圓于點D.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
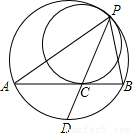
 已知;如圖,兩圓內切于點P,大圓的弦AB切小圓于點C,PC的延長線交大圓于點D.
已知;如圖,兩圓內切于點P,大圓的弦AB切小圓于點C,PC的延長線交大圓于點D.查看答案和解析>>
科目:初中數學 來源:2000年全國中考數學試題匯編《圖形的相似》(03)(解析版) 題型:解答題

查看答案和解析>>
科目:初中數學 來源:2000年全國中考數學試題匯編《圓》(07)(解析版) 題型:解答題
查看答案和解析>>
科目:初中數學 來源:2000年天津市中考數學試卷(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com