
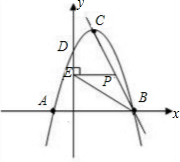
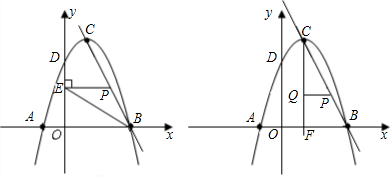
 如圖,在直角坐標系中,拋物線y=-x2+2x+c與y軸交于點D(0,3).
如圖,在直角坐標系中,拋物線y=-x2+2x+c與y軸交于點D(0,3).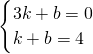 ,
,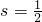 PE•OE=
PE•OE=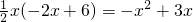
 )+
)+ =-(x-
=-(x- )2+
)2+ .
. 符合1<x<3,
符合1<x<3, 時,s取得最大值,最大值為
時,s取得最大值,最大值為 .
.
 ,
, 舍去).
舍去).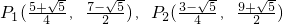 .
.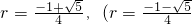 舍去).
舍去). .
.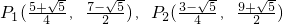 ,
, .
.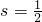 PE•OE=
PE•OE=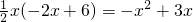 ,求出s最大值即可,再根據當⊙P與⊙C外切時,以及當⊙P與⊙C內切時,分別得出P點的坐標.
,求出s最大值即可,再根據當⊙P與⊙C外切時,以及當⊙P與⊙C內切時,分別得出P點的坐標.

 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,在直角坐標系中,點P的坐標為(3,4),將OP繞原點O逆時針旋轉90°得到線段OP′.
如圖,在直角坐標系中,點P的坐標為(3,4),將OP繞原點O逆時針旋轉90°得到線段OP′. | PP′ |
查看答案和解析>>
科目:初中數學 來源: 題型:
| 6 |
| x |
| 3 |
| 2 |
| 6 |
| x |

查看答案和解析>>
科目:初中數學 來源: 題型:
 ,2).畫出△ABC的兩個位似圖形△A1B1C1,△A2B2C2,同時滿足下列兩個條件:
,2).畫出△ABC的兩個位似圖形△A1B1C1,△A2B2C2,同時滿足下列兩個條件:查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com