
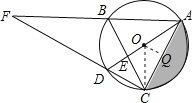
【題目】(本題滿分10分)如圖,△ABC是⊙O的內接三角形,AD是⊙O的直徑,∠ABC=60°,∠ACB=50°,請解答下列問題:

(1)求∠CAD的度數;
(2)設AD、BC相交于E,AB、CD的延長線相交于F,求∠AEC、∠AFC的度數;
(3)若AD=6,求圖中陰影部分的面積.
【答案】(1)30°;(2)∠AEC=100°,∠AFC=20°;(3)![]() .
.
【解析】試題分析:
(1)根據圓周角定理求出∠ADC、∠ACD的度數,相減即可;
(2)根據三角形的內角和定理求出∠BAC,根據三角形的外角性質求出即可;
(3)連接OC,過O作OQ⊥AC于Q,求出∠AOC的度數,求出高OQ和弦AC,求出扇形和三角形的面積,相減即可.
試題解析:
:(1)∵弧AC=弧AC,
∴∠ADC=∠ABC=60°,
∵AD是直徑,
∴∠ACD=90°,
∴∠CAD=180°-∠ACD-∠ADC=30°,
答:∠CAD的度數是30°.
(2)∵∠BAC=180°-∠ABC-∠ACB=70°,
∴∠BAD=∠BAC-∠CAD=70°-30°=40°,
∴∠BCD=∠BAD=40°,
∴∠AEC=∠ADC+∠BCD=100°,
∵∠AFC=∠ABC-∠BCF=60°-40°=20°,
答:∠AEC=100°,∠AFC=20°.
連接OC,過O作OQ⊥AC于Q,
∵∠CAD=30°,AO=3,
∴OQ=![]()
由勾股定理得:AQ=![]()
由垂徑定理得:AC=2AQ=![]()
∵∠AOC=2∠ABC=120°,
∴陰影部分的面積是S扇形OAC-S△AOC=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】(本題滿分6分)
小明和小亮做撲克游戲,桌面上放有兩堆牌,分別是紅桃和黑桃的1,2,3,4和黑桃的1,2,3,4。小明建議:“我從紅桃中抽取一張牌,你從黑桃中取一張,當兩張牌數字之積為奇數時,你得1分,為偶數我得1分,先得到10分的獲勝”。這個游戲對小亮和小明公平嗎?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了了解九年級上學期期末考試數學成績,從九年級學生中隨機抽取了部分學生進行調查,并將所抽取的學生數學成績(成績均為整數)分為A、B、C、D、E五個等級,A:50.5~60.5,B:60.5~70.5,C:70.5~80.5,D:80.5~90.5,E:90.5~100.5,并繪制了如圖所示的頻數分布直方圖和扇形統計圖,請你根據統計圖提供的信息解答下列問題: 
(1)這次抽樣調查共抽取了多少名學生?
(2)請把頻數分布直方圖補充完整;
(3)這次期末考試數學成績的中位數落在哪個等級內?
(4)該校九年級有800名學生,若規定80分以上(不含80分)為良好,試估計九年級有多少名學生的數學成績為良好?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=ax2+x+2經過點(-1,0).
(1)求a的值,并寫出這條拋物線的頂點坐標.
(2)若點P(t,t)在拋物線上,則點P叫做拋物線上的不動點,求出這個拋物線上所有不動點的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com