【答案】
分析:根據題意畫出圖形,如圖所示,由弦AB分圓為1:5兩部分,求出劣弧所對的圓心角∠AOB的度數,根據同弧所對的圓心角等于所對圓周角的2倍,求出劣弧所對的圓周角∠ACB的度數即為弦所對的一個圓周角度數;然后根據圓內接四邊形的對角互補,由∠ACB的度數求出∠ADB的度數,為優弧所對的圓周角,即為弦所對的另一個圓周角,綜上,得到弦所對的兩個圓周角的度數.
解答: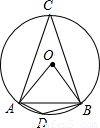
解:根據題意畫出圖形,如圖所示:
由弦AB分圓為1:5兩部分,得到
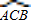
與
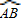
所對的圓心角度數之比為5:1,
∴劣弧所對的圓心角∠AOB=

×360°=60°,
又圓周角∠ACB和圓心角∠AOB都對
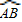
,
∴∠ACB=

∠AOB=30°;
∵四邊形ADBC為圓O的圓內接四邊形,
∴∠ACB+∠ADB=180°,
∴∠ADB=150°,
則弦AB所對的圓周角為30°或150°.
故答案為:30°或150°
點評:此題考查了圓周角定理,圓心角、弧及弦的關系,以及圓內接四邊形的性質.對圓周角及圓心角進行相互轉換是處理圓周角與圓心角問題時常用的方法,另外要求學生注意一條弦對著兩條弧,對著兩種圓周角.解答此類題往往借助圖形,利用分類討論的思想解決問題.

 解:根據題意畫出圖形,如圖所示:
解:根據題意畫出圖形,如圖所示: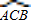 與
與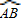 所對的圓心角度數之比為5:1,
所對的圓心角度數之比為5:1, ×360°=60°,
×360°=60°,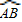 ,
, ∠AOB=30°;
∠AOB=30°;
