
【題目】涌泉鎮是中國無核蜜桔之鄉,已知某蜜桔種植大戶馮大爺的蜜桔成本為2元/千克,如果在未來90天蜜桔的銷售單價p(元/千克)與時間t(天)之間的函數關系式為p=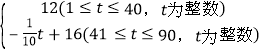 ,且蜜桔的日銷量y(千克)與時間t(天)滿足一次函數關系,其部分數據如下表所示:
,且蜜桔的日銷量y(千克)與時間t(天)滿足一次函數關系,其部分數據如下表所示:
時間t/天 | 1 | 10 | 20 | 40 | 70 | 90 |
日銷售量y/千克 | 105 | 150 | 200 | 300 | 450 | 550 |
(1)求y與t之間的函數表達式;
(2)在未來90天的銷售中,預測哪一天的日銷售利潤最大?最大日銷售利潤為多少元?
(3)在實際銷售的后50天中,馮大爺決定每銷售1千克蜜桔就捐贈n元利潤(n<5)給留守兒童作為助學金,銷售過程中馮大爺發現,恰好從第51天開始,和前一天相比,扣除捐贈后的日銷售利潤逐日減少,請求出n的取值范圍.
【答案】(1)y=5t+100;(2)前60天利潤最大,最大利潤為3200元;(3)n的取值范圍為1.9≤n<5.
【解析】
(1)運用待定系數法求出函數解析式;(2)設第x天的銷售利潤為w元.當1≤t≤40時,由題意w=(12-2)(5t+100)=50t+1000;當t=40時w最大值為3000元;當41≤t≤90時,w=(5t+100)(-![]() t+16-2)=-
t+16-2)=-![]() t2+60t+1400,再求函數最值;(3)設每天扣除捐贈后的日銷售利潤為m元.由題意m=(5t+100)(-
t2+60t+1400,再求函數最值;(3)設每天扣除捐贈后的日銷售利潤為m元.由題意m=(5t+100)(-![]() t+16-2)-(5t+100)n=-
t+16-2)-(5t+100)n=-![]() t2+(60-5n)t+1400-100n,根據實際得49.5≤60-5n<50.5,1.9<n≤2.1,可進一步求出n的取值范圍.
t2+(60-5n)t+1400-100n,根據實際得49.5≤60-5n<50.5,1.9<n≤2.1,可進一步求出n的取值范圍.
解:(1)設y=kt+b,把t=1,y=105;t=10,y=150代入得到:![]() ,
,
解得:![]() ,
,
∴y=5t+100;
(2)設第x天的銷售利潤為w元.
當1≤t≤40時,由題意w=(12-2)(5t+100)=50t+1000;
當t=40時w最大值為3000元;
當41≤t≤90時,w=(5t+100)(-![]() t+16-2)=-
t+16-2)=-![]() t2+60t+1400,
t2+60t+1400,
∵對稱軸t=60,a=-![]() <0,
<0,
∴在對稱軸左側w隨x增大而增大,
∴t=60時,w最大值=3200,
綜上所述前60天利潤最大,最大利潤為3200元.
(3)設每天扣除捐贈后的日銷售利潤為m元.
由題意m=(5t+100)(-![]() t+16-2)-(5t+100)n=-
t+16-2)-(5t+100)n=-![]() t2+(60-5n)t+1400-100n,
t2+(60-5n)t+1400-100n,
∵在后50天中,每天扣除捐贈后的日銷售利潤隨時間t的增大而減少,
∴49.5≤60-5n<50.5,
∴1.9<n≤2.1.
又∵n<5,
∴n的取值范圍為1.9≤n<5.


科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,弦CD⊥AB,垂足為點P,直線BF與AD的延長線交于點F,且∠AFB=∠ABC.
(1)求證:直線BF是⊙O的切線.
(2)若CD=2![]() ,OP=1,求線段BF的長.
,OP=1,求線段BF的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,將矩形OABC置于平面直角坐標系中,點A,C分別在x,y軸的正半軸上,已知點B(4,2),將矩形OABC翻折,使得點C的對應點P恰好落在線段OA(包括端點O,A)上,折痕所在直線分別交BC、OA于點D、E;若點P在線段OA上運動時,過點P作OA的垂線交折痕所在直線于點Q.
(1)求證:CQ=QP
(2)設點Q的坐標為(x,y),求y關于x的函數關系式及自變量x的取值范圍;
(3)如圖2,連結OQ,OB,當點P在線段OA上運動時,設三角形OBQ的面積為S,當x取何值時,S取得最小值,并求出最小值;
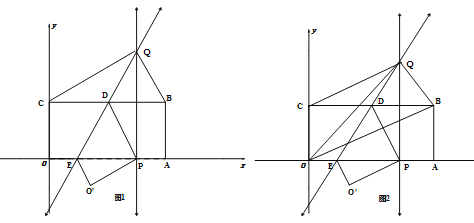
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB∥CD,BD平分∠ABC,CE平分∠DCF,∠ACE=90°.
(1)判斷BD和CE的位置關系,并說明理由;
(2)判斷AC和BD是否垂直,并說明理由.
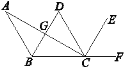
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“低碳環保,你我同行”.近幾年,各大城市的公共自行車給市民出行帶來了極大的方便.圖①是公共自行車的實物圖,圖②是公共自行車的車架示意圖,點A.D、C、E在同一條直線上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于點D,座桿CE=15cm,且∠EAB=75°.
(1)求AD的長;
(2)求點E到AB的距離.(參考數據:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)
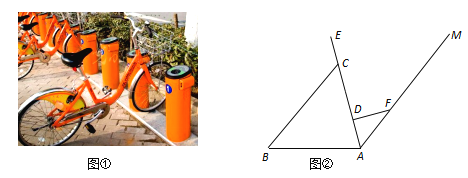
查看答案和解析>>
科目:初中數學 來源: 題型:
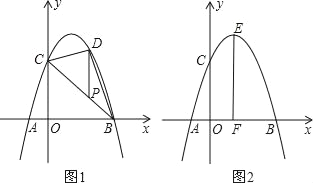
【題目】拋物線y=﹣x2+bx+c經過點A、B、C,已知A(﹣1,0),C(0,3).
(1)求拋物線的解析式;
(2)如圖1,P為線段BC上一點,過點P作y軸平行線,交拋物線于點D,當△BDC的面積最大時,求點P的坐標;
(3)如圖2,拋物線頂點為E,EF⊥x軸于F點,M(m,0)是x軸上一動點,N是線段EF上一點,若∠MNC=90°,請指出實數m的變化范圍,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
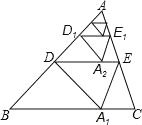
【題目】如圖,將△ABC沿著過AP中點D的直線折疊,使點A落在B C邊上的A1處,稱為第1次操作,折痕DE到BC的距離記為h1,還原紙片后,再將△ADE沿著過AD中點D1的直線折疊,使點A落在DE邊上的A2處,稱為第2次操作,折痕D1E1到BC的距離記為h2,按上述方法不斷操作下去…經過第2018次操作后得到的折痕D2017E2017到BC的距離記為h2018,若h1=1,則h2018的值為( )
A. 2﹣![]() B.
B. ![]() C. 1﹣
C. 1﹣![]() D. 2﹣
D. 2﹣![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】AB是⊙O的直徑,點E是弧BF的中點,連接AF交過E的切線于點D,AB的延長線交該切線于點C,若∠C=30°,⊙O的半徑是2,則圖形中陰影部分的面積是_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com