
【題目】如圖,![]() 是圓
是圓![]() 的直徑,
的直徑,![]() 是圓
是圓![]() 的切線,
的切線,![]() 交圓
交圓![]() 于點
于點![]() ,點
,點![]() 是
是![]() 的中點,連接
的中點,連接![]() .
.
(1)求證:![]()
(2)求證:![]() 四點共圓
四點共圓
(3)![]() 滿足什么條件時,經過
滿足什么條件時,經過![]() 的圓與
的圓與![]() 相切?并說明理由.
相切?并說明理由.
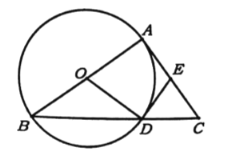
【答案】(1)見詳解;(2)見詳解;(3)等腰直角三角形.
【解析】
(1)連接AD,根據直徑所對的圓周角是直角,可證得∠ADB=90°,再利用鄰角互補的性質可得∠ADC=90°,再根據直角三角形斜邊上的中線等于斜邊的一半,可得AE=DE,由等邊對等角可證得∠DAE=∠ADE,又由OA=OD,可得∠OAD=∠ODA,從而有∠OAD+∠DAE =∠ODA+∠ADE,再由切線的性質可得∠OAD+∠DAE =90°,從而結論得證;
(2)欲證四點共圓,只須證得四點到某一點的距離相等即可;
(3)由(1)可知AD⊥BC,所以要使經過![]() 的圓與
的圓與![]() 相切,則AD必為直徑,由(2)可知OE必為直徑,從而易證四邊形OAED為正方形,從而有DE∥AB,且DE=
相切,則AD必為直徑,由(2)可知OE必為直徑,從而易證四邊形OAED為正方形,從而有DE∥AB,且DE=![]() AB,所以D為BC的中點,而AD⊥BC,故可知
AB,所以D為BC的中點,而AD⊥BC,故可知![]() 為等腰直角三角形.
為等腰直角三角形.
(1) 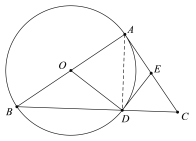
證明:如圖所示,連接AD,
∵![]() 是圓
是圓![]() 的切線,
的切線,
∴∠BAE=90°
∴∠BAD+∠DAE=90°,
∵![]() 是圓
是圓![]() 的直徑,
的直徑,
∴∠ADB=∠ADC=90°.
∵點![]() 是
是![]() 的中點,
的中點,
∴AE=DE.
∴∠DAE=∠ADE,
∴∠BAD+∠ADE =90°.
∵OD=OA,
∴∠BAD=∠ODA.
∴∠ODA+∠ADE =90°.
即∠ODE=90°.
∴![]() .
.
(2) 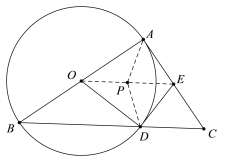
證明:如圖所示,連接OE,取OE的中點P,連接PA,PD.
由(1)可知∠OAE=ODE=90°,
∵點P是OE的中點,
∴PA=PO=PE=PD,
∴![]() 四點共圓.
四點共圓.
(3) 當![]() 是等腰直角三角形時,經過
是等腰直角三角形時,經過![]() 的圓與
的圓與![]() 相切.
相切.
理由如下:如圖所示:
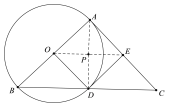
設⊙P為經過![]() 的圓.
的圓.
∵![]() 是等腰直角三角形,
是等腰直角三角形,
∴AB=AC,∠B=∠C=45°.
∵OB=OD,
∴∠B=∠ODB=45°.
∵O,E分別為AB,AC的中點,
∴OE∥BC.
∴∠POD=∠ODB=45°.
∵PO=PD,
∴∠PDO=∠POD=45°.
∴∠PDB=∠PDO+∠ODB =45°+45°=90°.
即PD⊥BC,
∴BC與圓P相切.
即當![]() 是等腰直角三角形時,經過
是等腰直角三角形時,經過![]() 的圓與
的圓與![]() 相切.
相切.


科目:初中數學 來源: 題型:
【題目】如圖,菱形ABCD中的邊長為1,∠BAD=60°,將菱形ABCD繞點A逆時針方向旋轉30°得到菱形AB′CD′,B′C′交CD于點E,連接AE,CC′,則下列結論:①ΔAB′E≌ΔADE;②EC=ED;③AE⊥CC′;④四邊形AB′ED的周長為![]() +2.其中正確結論的個數是
+2.其中正確結論的個數是
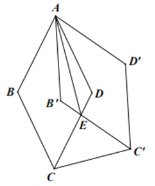
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司研制出新產品,該產品的成本為每件2400元.在試銷期間,購買不超過10件時,每件銷售價為3000元;購買超過10件時,每多購買一件,所購產品的銷售單價均降低5元,但最低銷售單價為2600元。請解決下列問題:
(1)直接寫出:購買這種產品 ________件時,銷售單價恰好為2600元;
(2)設購買這種產品x件(其中x>10,且x為整數),該公司所獲利潤為y元,求y與x之間的函數表達式;
(3)該公司的銷售人員發現:當購買產品的件數超過10件時,會出現隨著數量的增多,公司所獲利潤反而減少這一情況.為使購買數量越多,公司所獲利潤越大,公司應將最低銷售單價調整為多少元?(其它銷售條件不變)
查看答案和解析>>
科目:初中數學 來源: 題型:
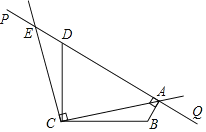
【題目】如圖,∠BCD=90°,且BC=DC,直線PQ經過點D.設∠PDC=α(45°<α<135°),BA⊥PQ于點A,將射線CA繞點C按逆時針方向旋轉90°,與直線PQ交于點E.
(1)當α=125°時,∠ABC= °;
(2)求證:AC=CE;
(3)若△ABC的外心在其內部,直接寫出α的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
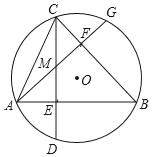
【題目】如圖,在圓O中,弦AB⊥CD于E,弦AG⊥BC于F,CD與AG相交于點M.
(1)求證:弧BD=弧BG.
(2)如果AB=12,CM=4,求圓O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程![]()
(1)求證:不論k取什么實數值,這個方程總有實數根;
(2)若等腰三角形ABC的一邊長為![]() ,另兩邊的長b、c恰好是這個方程的兩個根,求△ABC的周長.
,另兩邊的長b、c恰好是這個方程的兩個根,求△ABC的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】雅安地震牽動著全國人民的心,某單位開展了“一方有難,八方支援”賑災捐款活動.第一天收到捐款10 000元,第三天收到捐款12 100元.
(1)如果第二天、第三天收到捐款的增長率相同,求捐款增長率;
(2)按照(1)中收到捐款的增長速度,第四天該單位能收到多少捐款?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】八年級一班開展了“讀一本好書”的活動,班委會對學生閱讀書籍的情況進行了問卷調查,問卷設置了“小說”“戲劇”“散文”“其他”四個類型,每位同學僅選一項,根據調查結果繪制了不完整的頻數分布表和扇形統計圖.
類別 | 頻數(人數) | 頻率 |
小說 | 0.5 | |
戲劇 | 4 | |
散文 | 10 | 0.25 |
其他 | 6 | |
合計 | 1 |
根據圖表提供的信息,解答下列問題:
(1)八年級一班有多少名學生?
(2)請補全頻數分布表,并求出扇形統計圖中“其他”類所占的百分比;
(3)在調查問卷中,甲、乙、丙、丁四位同學選擇了“戲劇”類,現從以上四位同學中任意選出2名同學參加學校的戲劇興趣小組,請用畫樹狀圖或列表法的方法,求選取的2人恰好是乙和丙的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
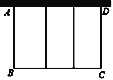
【題目】如圖,現有長度100米的圍欄,要利用一面墻(墻長為25米)建羊圈,BC的長度不大于墻長。
⑴可以圍成總面積為400平方米的三個大小相同的矩形羊圈?如果能,求羊圈的邊長AB,BC各為多少米?如果不能,請說明理由。
⑵可以圍成總面積為640平方米的三個大小相同的矩形羊圈?如果能,求羊圈的邊長AB,BC各為多少米?如果不能,請說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com