
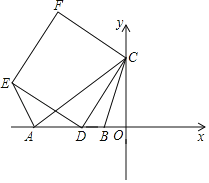
【題目】如圖,在平面直角坐標系中,點A、B在x軸上,點C在y軸上,AB=BC=5,AC=8,D為線段AB上一動點,以CD為邊在x軸上方作正方形CDEF,連接AE.
(1)若點B的坐標為(m,0),則m= ;
(2)當BD= 時,EA⊥x軸;
(3)當點D由點B運動到點A過程中,點F經過的路徑長為 ;
(4)當△ADE面積最大時,求出BD的長及△ADE面積最大值.
【答案】(1)﹣![]() ;(2)
;(2)![]() ;(3)5;(4)BD=
;(3)5;(4)BD=![]() ,△ADE面積最大值為
,△ADE面積最大值為![]()
【解析】
(1)由勾股定理可得64﹣(5﹣m)2=25﹣(﹣m)2,可求m的值;
(2)由勾股定理可求CO的長,由“AAS”可證△AED≌△ODC,可得AD=CO,即可求解;
(3)由“AAS”可證△CFH≌△CDO,可得CH=CO=![]() ,FH=DO,可得點F在FH上移動,由特殊位置可求解;
,FH=DO,可得點F在FH上移動,由特殊位置可求解;
(4)過點E作EN⊥x軸于點N,由三角形的面積公式可得△ADE面積=![]() ×AD×EN=
×AD×EN=![]() (5﹣BD)(
(5﹣BD)(![]() +BD)=﹣
+BD)=﹣![]() (BD﹣
(BD﹣![]() )2+
)2+![]() ,由二次函數的性質可求解.
,由二次函數的性質可求解.
解:(1)∵點B的坐標為(m,0),
∴BO=﹣m,
∵CO2=AC2﹣AO2,CO2=CB2﹣BO2,
∴64﹣(5﹣m)2=25﹣(﹣m)2,
∴m=﹣![]() ,
,
故答案為:﹣![]() ;
;
(2)∵點B的坐標為(﹣![]() ,0),
,0),
∴BO=![]() ,
,
∴CO=![]() =
=![]() ,
,
∵EA⊥x軸,
∴∠EAD=90°,
∴∠EDA+∠AED=90°,
∵四邊形CDEF是正方形,
∴CD=DE,∠EDC=90°,
∴∠EDA+∠CDO=90°,
∴∠AED=∠CDO,
∵∠EAD=∠COD,ED=CD,
∴△AED≌△ODC(AAS)
∴AE=DO,AD=CO=![]() ,
,
∴BD=AB﹣AD=5﹣![]() =
=![]() ,
,
∴當BD=![]() 時,EA⊥x軸;
時,EA⊥x軸;
故答案為:![]() ;
;
(3)如圖,過點C作CH⊥y軸,過點F作FH⊥CH,交點為H,

∵四邊形CDEF是正方形,
∴CD=CF,∠FCD=90°,
∴∠FCH+∠DCH=90°,
又∵∠DCO+∠HCD=90°,
∴∠FCH=∠DCO,
又∵FC=DC,∠CHF=∠DOC=90°,
∴△CFH≌△CDO(AAS)
∴CH=CO=![]() ,FH=DO,
,FH=DO,
∴點F在FH上移動,
當點D與點B重合時,FH=BO=![]() ,
,
當點D與點BC重合時,FH=AO=AB+BO=5+![]() =
=![]() ,
,
∴當點D由點B運動到點A過程中,點F經過的路徑長為![]() ﹣
﹣![]() =5,
=5,
故答案為:5;
(4)如圖,過點E作EN⊥x軸于點N,

由(2)可得△DEN≌△CDO,
∴EN=DO,
∵△ADE面積=![]() ×AD×EN=
×AD×EN=![]() (5﹣BD)(
(5﹣BD)(![]() +BD)=﹣
+BD)=﹣![]() (BD﹣
(BD﹣![]() )2+
)2+![]() ,
,
∴當BD=![]() 時,△ADE面積最大值為
時,△ADE面積最大值為![]() .
.


 波波熊暑假作業江西人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案 學而優暑期銜接南京大學出版社系列答案
學而優暑期銜接南京大學出版社系列答案 Happy holiday歡樂假期暑假作業廣東人民出版社系列答案
Happy holiday歡樂假期暑假作業廣東人民出版社系列答案科目:初中數學 來源: 題型:
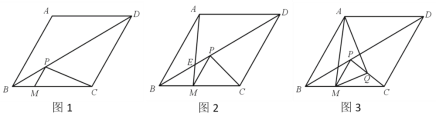
【題目】已知菱形ABCD中,∠ABC=60°,AB=4,點M在BC邊上,過點M作PM∥AB交對角線BD于點P,連接PC.
(1)如圖1,當BM=1時,求PC的長;
(2)如圖2,設AM與BD交于點E,當∠PCM=45°時,求證:![]() =
=![]() ;
;
(3)如圖3,取PC的中點Q,連接MQ,AQ.
①請探究AQ和MQ之間的數量關系,并寫出探究過程;
②△AMQ的面積有最小值嗎?如果有,請直接寫出這個最小值;如果沒有,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
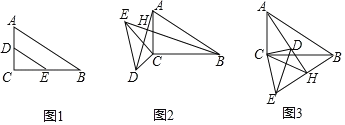
【題目】已知:已知Rt△ABC中,∠ACB=90°,D、E分別是AC、BC上的點,連DE,且![]() ,tanB
,tanB![]() ,如圖1.
,如圖1.
(1)如圖2,將△CDE繞C點旋轉,連AD、BE交于H,求證:AD⊥BE;
(2)如圖3,當△CDE繞C點旋轉過程中,當CH![]() 時,求
時,求![]() AH﹣BH的值;
AH﹣BH的值;
(3)若CD=1,當△CDE繞C點旋轉過程中,直接寫出AH的最大值是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學全體同學參加了“關懷貧困學生”愛心捐款活動,該校隨機抽查了七、八、九三個年級部分學生捐款情況,將結果繪制成兩幅不完整的統計圖.根據圖中的信息,解決下列問題:
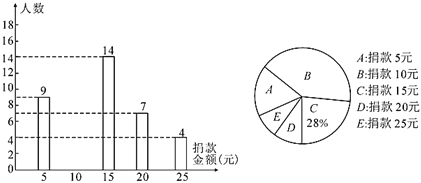
(1)這次共抽查了_______名學生進行統計,其中![]() 類所對應扇形的圓心角的度數為________;
類所對應扇形的圓心角的度數為________;
(2)將條形統計圖補充完整;
(3)該校有![]() 名學生,估計該校捐款
名學生,估計該校捐款![]() 元的學生有多少人?
元的學生有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的盒子中裝有4張卡片.4張卡片的正面分別標有數字1,2,3,4,這些卡片除數字外都相同,將卡片攪勻.
(1)從盒子任意抽取一張卡片,恰好抽到標有奇數卡片的概率是: ;
(2)先從盒子中任意抽取一張卡片,再從余下的3張卡片中任意抽取一張卡片,求抽取的2張卡片標有數字之和大于4的概率(請用畫樹狀圖或列表等方法求解).
查看答案和解析>>
科目:初中數學 來源: 題型:
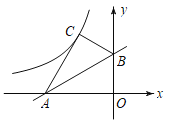
【題目】如圖,已知直線![]() 與x軸,y軸分別交于點A,B,將△ABO沿直線AB翻折后得到△ABC,若反比例函數
與x軸,y軸分別交于點A,B,將△ABO沿直線AB翻折后得到△ABC,若反比例函數![]() (x<0)的圖象經過點C,則k=______.
(x<0)的圖象經過點C,則k=______.
查看答案和解析>>
科目:初中數學 來源: 題型:
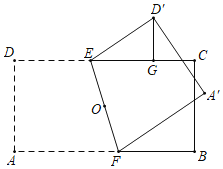
【題目】如圖,點O是矩形ABCD的對角線的交點,AB=15,BC=8,直線EF經過點O,分別與邊CD,AB相交于點E,F(其中0<DE<![]() ).現將四邊形ADEF沿直線EF折疊得到四邊形A′D′EF,點A,D的對應點分別為A′,D′,過D′作D′G⊥CD于點G,則線段D′G的長的最大值是_____,此時折痕EF的長為_____.
).現將四邊形ADEF沿直線EF折疊得到四邊形A′D′EF,點A,D的對應點分別為A′,D′,過D′作D′G⊥CD于點G,則線段D′G的長的最大值是_____,此時折痕EF的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
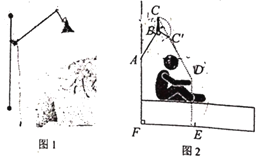
【題目】如圖1是一款創意型壁燈,示意圖如圖2所示,∠BAF=150°,燈臂BC=0.2米,不使用時BC‖AF,人在床上閱讀時,將![]() 繞點B旋轉至
繞點B旋轉至![]() ,
,![]() ,書本到地面距離DE=1米,C,
,書本到地面距離DE=1米,C,![]() ,D三點恰好在同一直線上,且
,D三點恰好在同一直線上,且![]() ,則此時固定點A到地面的距離
,則此時固定點A到地面的距離![]() ________米.
________米.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com