
【題目】某學習小組在研究函數y= ![]() x3﹣2x的圖象與性質時,已列表、描點并畫出了圖象的一部分.
x3﹣2x的圖象與性質時,已列表、描點并畫出了圖象的一部分.
x | … | ﹣4 | ﹣3.5 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
y | … | ﹣ | ﹣ |
|
|
| 0 | ﹣ | ﹣ | ﹣ |
|
| … |
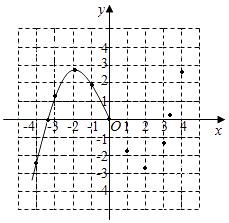
(1)請補全函數圖象;
(2)方程 ![]() x3﹣2x=﹣2實數根的個數為;
x3﹣2x=﹣2實數根的個數為;
(3)觀察圖象,寫出該函數的兩條性質.
【答案】
(1)解:補全函數圖象如圖所示,
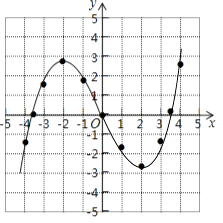
(2)3
(3)解:由圖象知,
①此函數在實數范圍內既沒有最大值,也沒有最小值,
②此函數在x<﹣2和x>2,y隨x的增大而增大,
③此函數圖象過原點,
④此函數圖象關于原點對稱.
【解析】
( 2 )如圖1,
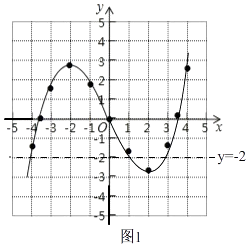
作出直線y=﹣2的圖象,
由圖象知,函數y= ![]() x3﹣2x的圖象和直線y=﹣2有三個交點,
x3﹣2x的圖象和直線y=﹣2有三個交點,
∴方程 ![]() x3﹣2x=﹣2實數根的個數為3,
x3﹣2x=﹣2實數根的個數為3,
所以答案是:3.
【考點精析】根據題目的已知條件,利用二次函數的圖象和二次函數的性質的相關知識可以得到問題的答案,需要掌握二次函數圖像關鍵點:1、開口方向2、對稱軸 3、頂點 4、與x軸交點 5、與y軸交點;增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小.


科目:初中數學 來源: 題型:
【題目】已知:如圖1,射線OP∥AE,∠AOP的角平分線交射線AE于點B.
(1)若∠A=50°,求∠ABO的度數;
(2)如圖2,若點C在射線AE上,OB平分∠AOC交AE于點B,OD平分∠COP交AE于點D,∠ABO-∠AOB=70°,求∠ADO的度數;
(3)如圖3,若∠A=α,依次作出∠AOP的角平分線OB,∠BOP的角平分線OB1,∠B1OP的角平分線OB2,…,∠Bn-1OP的角平分線OBn,其中點B,B1,B2,…,Bn-1,Bn都在射線AE上,試求∠ABnO的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下面三行數:
第1列 | 第2列 | 第3列 | 第4列 | … | 第n列 |
﹣3 | 9 | a | 81 | … | r |
1 | ﹣3 | 9 | b | … | s |
﹣2 | 10 | c | 82 | … | t |
(1)直接寫出a,b,c的值;
(2)直接寫出r,s,t的值;
(3)設x,y,z分別為第①②③行的第2019個數,求x+6y+z的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形OABC是平行四邊形,點C在x軸上,反比例函數y= ![]() (x>0)的圖象經過點A(5,12),且與邊BC交于點D.若AB=BD,則點D的坐標為 .
(x>0)的圖象經過點A(5,12),且與邊BC交于點D.若AB=BD,則點D的坐標為 . 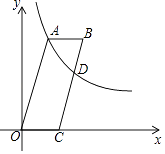
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在“宏揚傳統文化,打造書香校園”活動中,學校計劃開展四項活動:“A﹣國學誦讀”、“B﹣演講”、“C﹣課本劇”、“D﹣書法”,要求每位同學必須且只能參加其中一項活動,學校為了了解學生的意愿,隨機調查了部分學生,結果統計如下:
(1)如圖,希望參加活動C占20%,希望參加活動B占15%,則被調查的總人數為 人,扇形統計圖中,希望參加活動D所占圓心角為 度,根據題中信息補全條形統計圖.
(2)學校現有800名學生,請根據圖中信息,估算全校學生希望參加活動A有多少人?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某服裝店購進一批甲、乙兩種款型時尚T恤衫,甲種款型共用了7800元,乙種款型共用了6400元,甲種款型的件數是乙種款型件數的1.5倍,甲種款型每件的進價比乙種款型每件的進價少30元.
(1)甲、乙兩種款型的T恤衫各購進多少件?
(2)商店進價提高60%標價銷售,銷售一段時間后,甲款型全部售完,乙款型剩余一半,商店決定對乙款型按標價的五折降價銷售,很快全部售完,求售完 這批T恤衫商店共獲利多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料:
小明遇到這樣問題:
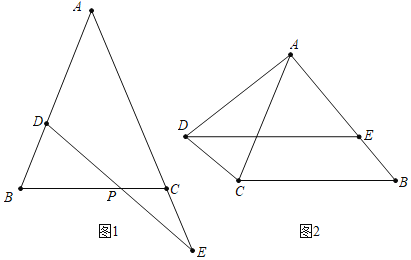
如圖1,在![]() 中,
中,![]() ,在AB上取一點D,在AC延長線上取一點E,若
,在AB上取一點D,在AC延長線上取一點E,若![]() ,判斷PD與PE的數量關系.
,判斷PD與PE的數量關系.
小明通過思考發現,可以采用兩種方法解決向題:
方法一:過點D作![]() ,交BC于F,即可解決向題;
,交BC于F,即可解決向題;
方法二:過點D、點E分別向直線BC引垂錢,垂足分別是F、G,也可解決問題.
![]() 請回答:PD與PE的數量關系是______;
請回答:PD與PE的數量關系是______;
![]() 任選上述兩種方法中的一種方法,在圖1中補全圖象,并給出證明;
任選上述兩種方法中的一種方法,在圖1中補全圖象,并給出證明;
參考小明思考問題的方法,解決問題:
![]() 如圖2,在
如圖2,在![]() 中,
中,![]() ,將AC繞點A順時針旋轉
,將AC繞點A順時針旋轉![]() 度后得到AD,過點D作
度后得到AD,過點D作![]() ,交AB于點E,
,交AB于點E,![]() ,則圖中是否存在與DE相等的線段,請找出來并給出證明.
,則圖中是否存在與DE相等的線段,請找出來并給出證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在四邊形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,點P從點A出發,沿折線ABCD方向以3cm/s的速度勻速運動;點Q從點D出發,沿線段DC方向以2cm/s的速度勻速運動. 已知兩點同時出發,當一個點到達終點時,另一點也停止運動,設運動時間為t(s).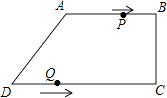
(1)求CD的長;
(2)當四邊形PBQD為平行四邊形時,求四邊形PBQD的周長;
(3)在點P、Q的運動過程中,是否存在某一時刻,使得△BPQ的面積為20cm2?若存在,請求出所有滿足條件的t的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com