
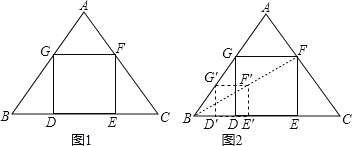
【題目】如圖,△ABC是一塊等邊三角形的廢鐵片,其中AB=AC=10![]() ,BC=12
,BC=12![]() .利用其剪裁一個正方形DEFG,使正方形的一條邊DE落在BC上,頂點F. G分別落在AC、AB上.
.利用其剪裁一個正方形DEFG,使正方形的一條邊DE落在BC上,頂點F. G分別落在AC、AB上.
(1)小聰想:要畫出正方形DEFG,只要能計算出正方形的邊長就能求出BD和CE的長,從而確定D點和E點,再畫正方形DEFG就容易了.請你幫小聰求出正方形的邊長.
(2)小明想:不求正方形的邊長也能畫出正方形.具體作法是:
①在AB邊上任取一點G′,如圖2作正方形G′D′E′F′;
②連接BF′并延長交AC于點F;
③過點F作FE∥F′E′交BC于點E,FG∥F′G′交AB于點G,GD∥G′D′交BC于點D,則四邊形DEFG即為所求的正方形.你認為小明的作法正確嗎?說明理由.
科目:初中數學 來源: 題型:
【題目】如圖,△ABC的周長為19,點D,E在邊BC上,∠ABC的平分線垂直于AE,垂足為N,∠ACB的平分線垂直于AD,垂足為M,若BC=7,則MN的長度為( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中數學 來源: 題型:
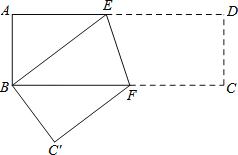
【題目】如圖,在矩形紙片ABCD中,AB=4cm,AD=8cm,按如圖方式折疊,使點D與點B重合,折痕為EF,則tan∠BEF=( )
A.2B.3C.4D.5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=3,BC=4,將矩形ABCD繞點C按順時針方向旋轉α角,得到矩形A'B'C'D',B'C與AD交于點E,AD的延長線與A'D'交于點F.

(1)如圖①,當α=60°時,連接DD',求DD'和A'F的長;
(2)如圖②,當矩形A'B'CD'的頂點A'落在CD的延長線上時,求EF的長;
(3)如圖③,當AE=EF時,連接AC,CF,求ACCF的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=3cm,AD=4cm,EF經過對角線BD的中點O,分別交AD,BC于點E,F.
(1)求證:△BOF≌△DOE;
(2)當EF⊥BD時,求AE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
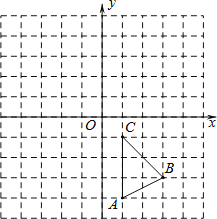
【題目】如圖,在平面直角坐標系中,△ABC的三個頂點坐標分別為A(1,﹣4)、B(3,﹣3)、C(1,﹣1)(每個小方格都是邊長為一個單位長度的正方形).
(1)請畫出△ABC關于原點對稱的△A1B1C1,并寫出A1,B1,C1的坐標;
(2)請畫出△ABC繞點B逆時針旋轉90°后的△A2B2C2.
查看答案和解析>>
科目:初中數學 來源: 題型:
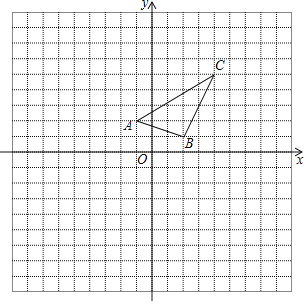
【題目】如圖,在邊長為1的正方形網格中建立平面直角坐標系,已知△ABC三個頂點分別為A(﹣1,2)、B(2,1)、C(4,5).
(1)以原點O為位似中心,在x軸的上方畫出△A1B1C1,使△A1B1C1與△ABC位似,且相似比為2;
(2)△A1B1C1的面積是 平方單位.
(3)點P(a,b)為△ABC內一點,則在△A1B1C1內的對應點P’的坐標為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1),在![]() 中,
中,![]() ,點
,點![]() 分別是邊
分別是邊![]() 的中點,連接
的中點,連接![]() .
.

(1)如圖①,求![]() 的值;
的值;
(2)將![]() 繞點
繞點![]() 順時針旋轉到如圖(2)的位置時,
順時針旋轉到如圖(2)的位置時,![]() 的大小是否發生變化,若不變化,請說明理由;若發生變化,請求出它的值;
的大小是否發生變化,若不變化,請說明理由;若發生變化,請求出它的值;
(3)將![]() 繞點
繞點![]() 順時針旋轉到直線
順時針旋轉到直線![]() 的下方,且
的下方,且![]() 在同一直線上時,如圖(3),求線段
在同一直線上時,如圖(3),求線段![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com