

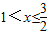 時,△PMN是鈍角三角形,不可能是直角三角形.
時,△PMN是鈍角三角形,不可能是直角三角形. .
. ,可過P作PP2⊥AB與P2,那么PP2的長可在直角三角形PP2M中,根據PM的長和∠BME的正弦值求出,進而可根據三角形的面積公式求出S、x的函數關系式.
,可過P作PP2⊥AB與P2,那么PP2的長可在直角三角形PP2M中,根據PM的長和∠BME的正弦值求出,進而可根據三角形的面積公式求出S、x的函數關系式. ≤x≤3,解法同上.
≤x≤3,解法同上.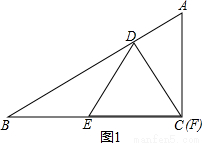 (1)解:當F點與C點重合時,如圖1所示:
(1)解:當F點與C點重合時,如圖1所示: BC=3;
BC=3;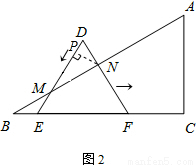
 ,
,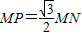 ,
,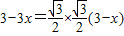 ,
,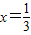 ,
,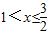 時,△PMN是鈍角三角形,不可能是直角三角形,
時,△PMN是鈍角三角形,不可能是直角三角形, 時,△PMN是直角三角形.
時,△PMN是直角三角形.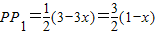 ,
, ×
×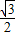 (3-x)×
(3-x)× (1-x),
(1-x),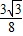 (x2-4x+3),
(x2-4x+3),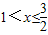 時,過P點作PP2⊥AB,垂足為P2,
時,過P點作PP2⊥AB,垂足為P2,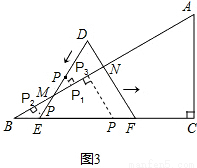
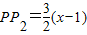 ,
, ×
×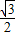 (3-x)×
(3-x)× (x-1),
(x-1),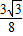 (x2-4x+3);
(x2-4x+3);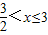 時,過P點作PP3⊥AB,垂足為P3,
時,過P點作PP3⊥AB,垂足為P3,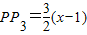 ,
, ×
×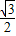 (3-x)×
(3-x)× (x-1),
(x-1),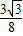 (x2-4x+3),
(x2-4x+3),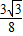 (x-2)2+
(x-2)2+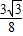 ,
,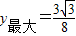 ,
, ×3×
×3× ×
×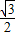 =
=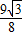 ,
,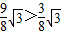 ,
,

 輕巧奪冠周測月考直通中考系列答案
輕巧奪冠周測月考直通中考系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com