
 ,正方形OABC內接于扇形,點A、C、B分別在OM、ON、
,正方形OABC內接于扇形,點A、C、B分別在OM、ON、 上,過作ME⊥CB交CB的延長線于E,則圖中陰影部分的面積為 .
上,過作ME⊥CB交CB的延長線于E,則圖中陰影部分的面積為 .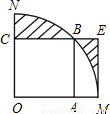
 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:初中數學 來源:101網校同步練習 初三數學 人教版(新課標2004年初審) 人教實驗版 題型:044
如圖,在半徑是2的圓O中,點Q為優弧![]() 的中點,圓心角∠MON=60°,在
的中點,圓心角∠MON=60°,在![]() 上有一動點P,且點P到弦MN的距離為x.
上有一動點P,且點P到弦MN的距離為x.

(1)求弦MN的長;
(2)試求陰影部分面積y與x的函數關系式,并寫出自變量x的取值范圍;
(3)試分析比較,當自變量x為何值時,陰影部分面積y與S扇形OMN的大小關系.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com