
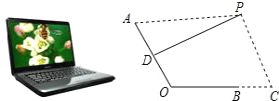
【題目】如圖是一臺放置在水平桌面上的筆記本電腦,將其側面抽象成如右圖所示的幾何圖形,若顯示屏所在面的側邊AO與鍵盤所在面的側邊BO長均為24cm,點P為眼睛所在位置,D為AO的中點,連接PD,當PD?AO時,稱點P為“最佳視角點”,作PC?BC,垂足C在OB的延長線上,且BC=12cm.
(1)當PA=45cm時,求PC的長;
(2)若?AOC=120°時,“最佳視角點”P在直線PC上的位置會發生什么變化?此時PC的長是多少?請通過計算說明.(結果精確到0.1cm,可用科學計算器,參考數據: ![]() ,
, ![]() )
)
【答案】(1)27cm;(2)位置上升了.34.7cm.
【解析】試題分析:(1)連結PO.先由線段垂直平分線的性質得出PO=PA=45cm,則OC=OB+BC=12+24=36cm,然后利用勾股定理即可求出PC=![]() =27cm;(2)過D作DE⊥OC交BO延長線于E,過D作DF⊥PC于F,則四邊形DECF是矩形.先解Rt△DOE,求出DE=DOsin60°=6
=27cm;(2)過D作DE⊥OC交BO延長線于E,過D作DF⊥PC于F,則四邊形DECF是矩形.先解Rt△DOE,求出DE=DOsin60°=6![]() ,EO=
,EO=![]() DO=6,則FC=DE=6
DO=6,則FC=DE=6![]() ,DF=EC=EO+OB+BC=42.再解Rt△PDF,求出PF=DFtan30°=42×
,DF=EC=EO+OB+BC=42.再解Rt△PDF,求出PF=DFtan30°=42×![]() =14
=14![]() ,則PC=PF+FC=14
,則PC=PF+FC=14![]() +6
+6![]() =20
=20![]() ≈34.68>27,即可得出結論.
≈34.68>27,即可得出結論.
試題解析:(1)當PA=45cm時,連結PO.如圖:
 ∵D為AO的中點,PD⊥AO,∴PO=PA=45cm.∵BO=24cm,BC=12cm,∠C=90°,∴OC=OB+BC=36cm,PC=
∵D為AO的中點,PD⊥AO,∴PO=PA=45cm.∵BO=24cm,BC=12cm,∠C=90°,∴OC=OB+BC=36cm,PC=![]() =27cm;(2)當∠AOC=120°,過D作DE⊥OC交BO延長線于E,過D作DF⊥PC于F,如圖:
=27cm;(2)當∠AOC=120°,過D作DE⊥OC交BO延長線于E,過D作DF⊥PC于F,如圖:
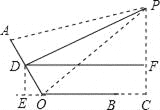 ,則四邊形DECF是矩形.在Rt△DOE中,∵∠DOE=60°,DO=
,則四邊形DECF是矩形.在Rt△DOE中,∵∠DOE=60°,DO=![]() AO=12,
AO=12,
∴DE=DOsin60°=6![]() ,EO=
,EO=![]() DO=6,∴FC=DE=6
DO=6,∴FC=DE=6![]() ,DF=EC=EO+OB+BC=6+24+12=42.在Rt△PDF中,∵∠PDF=30°,∴PF=DFtan30°=42×
,DF=EC=EO+OB+BC=6+24+12=42.在Rt△PDF中,∵∠PDF=30°,∴PF=DFtan30°=42×![]() =14
=14![]() ,∴PC=PF+FC=14
,∴PC=PF+FC=14![]() +6
+6![]() =20
=20![]() ≈34.68cm>27cm,∴點P在直線PC上的位置上升了.
≈34.68cm>27cm,∴點P在直線PC上的位置上升了.


 步步高達標卷系列答案
步步高達標卷系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com