
【題目】如圖,在平面直角坐標系中,矩形![]() 的頂點
的頂點![]() 在
在![]() 軸的正半軸上,
軸的正半軸上,![]() .對角線
.對角線![]() 相交于點
相交于點![]() ,反比例函數
,反比例函數![]() 的圖像經過點
的圖像經過點![]() ,分別與
,分別與![]() 交于點
交于點![]() .
.
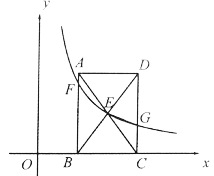
(1)若![]() ,求
,求![]() 的值;
的值;
(2)連接![]() ,若
,若![]() ,求
,求![]() 的面積.
的面積.
【答案】(1)k=20;(2)△CEG的面積為![]() .
.
【解析】
(1)先利用矩形的性質和線段中點坐標公式得到E(5,4),然后把E點坐標代入![]() 可求得k的值;
可求得k的值;
(2)利用勾股定理計算出AC=10,則BE=EC=5,所以BF=7,設OB=t,則F(t,7),E(t+3,4),利用反比例函數圖象上點的坐標得到7t=4(t+3),解得t=4,從而得到反比例函數解析式為y=![]() ,然后確定G點坐標,最后利用三角形面積公式計算△CEG的面積.
,然后確定G點坐標,最后利用三角形面積公式計算△CEG的面積.
(1)∵在矩形ABCD的頂點B,AB=8,BC=6,
而OC=8,
∴B(2,0),A(2,8),C(8,0),
∵對角線AC,BD相交于點E,
∴點E為AC的中點,
∴E(5,4),
把E(5,4)代入y=![]() 得k=5×4=20;
得k=5×4=20;
(2)∵AC=![]() =10,
=10,
∴BE=EC=5,
∵BF﹣BE=2,
∴BF=7,
設OB=t,則F(t,7),E(t+3,4),
∵反比例函數y=![]() (x>0)的圖象經過點E、F,
(x>0)的圖象經過點E、F,
∴7t=4(t+3),解得t=4,
∴k=7t=28,
∴反比例函數解析式為y=![]() ,
,
當x=10時,y=![]() ,
,
∴G(10,![]() ),
),
∴△CEG的面積=![]() .
.


 口算能手系列答案
口算能手系列答案科目:初中數學 來源: 題型:
【題目】新冠肺炎疫情期間,某小區計劃購買甲、乙兩種品牌的消毒劑,乙品牌消毒劑每瓶的價格比甲品牌消毒劑每瓶價格的3倍少50元,已知用300元購買甲品牌消毒劑的數量與用400元購買乙品牌消毒劑的數量相同.
(1)求甲、乙兩種品牌消毒劑每瓶的價格各是多少元?
(2)若該小區從超市一次性購買甲、乙兩種品牌的消毒劑共40瓶,且總費用為1400元,求購買了多少瓶乙品牌消毒劑?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校為了增強學生體質,決定開設以下體育課外活動項目:A:籃球 B:乒乓球C:羽毛球 D:足球,為了解學生最喜歡哪一種活動項目,隨機抽取了部分學生進行調查,并將調查結果繪制成了兩幅不完整的統計圖,請回答下列問題:


(1)這次被調查的學生共有 人;
(2)請你將條形統計圖(2)補充完整;
(3)在平時的乒乓球項目訓練中,甲、乙、丙、丁四人表現優秀,現決定從這四名同學中任選兩名參加乒乓球比賽,求恰好選中甲、乙兩位同學的概率(用樹狀圖或列表法解答)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線![]() 與
與![]() 軸和
軸和![]() 軸分別交于點
軸分別交于點![]() 和點
和點![]() 拋物線
拋物線![]() 經過點
經過點![]() 與直線
與直線![]() 的另一個交點為
的另一個交點為![]() .
.
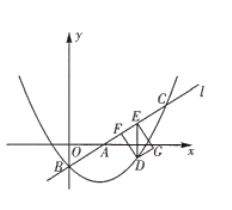
![]() 求
求![]() 的值和拋物線的解析式
的值和拋物線的解析式
![]() 點
點![]() 在拋物線上,
在拋物線上,![]() 軸交直線
軸交直線![]() 于點
于點![]() 點
點![]() 在直線
在直線![]() 上,且四邊形
上,且四邊形![]() 為矩形.設點
為矩形.設點![]() 的橫坐標為
的橫坐標為![]() 矩形
矩形![]() 的周長為
的周長為![]() 求
求![]() 與
與![]() 的函數關系式以及
的函數關系式以及![]() 的最大值
的最大值
![]() 將
將![]() 繞平面內某點
繞平面內某點![]() 逆時針旋轉
逆時針旋轉![]() 得到
得到![]() (點
(點![]() 分別與
分別與![]() 點對應),若
點對應),若![]() 的兩個頂點恰好落在拋物線上,請直接寫出點
的兩個頂點恰好落在拋物線上,請直接寫出點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是“經過已知直線外一點作這條直線的平行線”的尺規作圖過程.
己知:如圖1,直線![]() 和直線
和直線![]() 外一點
外一點![]() .
.
求作:直線![]() 的平行直線,使它經過點
的平行直線,使它經過點![]() .
.

作法:如圖2,
(1)過![]() 作直線
作直線![]() 與直線
與直線![]() 交于點
交于點![]() ;
;
(2)在直線![]() 取一點
取一點![]() ,以點
,以點![]() 為圓心,
為圓心,![]() 長為半徑畫弧,與直線
長為半徑畫弧,與直線![]() 交于點
交于點![]() ;
;
(3)以點![]() 為圓心,
為圓心,![]() 長為半徑畫弧,交直線
長為半徑畫弧,交直線![]() 于點
于點![]() 以點
以點![]() 為圓心,
為圓心,![]() 長為半徑畫弧,兩弧交于點
長為半徑畫弧,兩弧交于點![]() ;
;
(4)作直線![]() .
.
所以,直線![]() 就是所求作的平行線.
就是所求作的平行線.
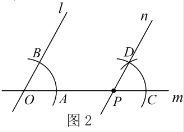
請回答:該作圖的依據是______________________________________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠BAC=90°,D是BC的中點,連接AD,E為AD的中點,過A作AF∥BC交BE延長線于F,連接CF.
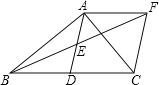
(1)求證:四邊形ADCF是菱形;
(2)在不添加任何輔助線的情況下,請直接寫出與△ACD面積相等的三角形(不包含△ACD).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的布袋中裝有相同的三個小球,其上面分別標注數字1、2、3、,現從中任意摸出一個小球,將其上面的數字作為點M的橫坐標;將球放回袋中攪勻,再從中任意摸出一個小球,將其上面的數字作為點M的縱坐標.
(1)求點M在直線y=x上的概率;
(2)求點M的橫坐標與縱坐標之和是偶數的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com