日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 初中數學 > 題目詳情

解答：

如圖，在△ABC所在平面中畫一條直線，使得與∠A成同旁內角的角有4個．

練習冊系列答案
相關習題

科目：初中數學 來源： 題型：

注意：為了使學生更好地解答本題，我們提供了一種解題思路，你可以依照這個思路按下面的要求填空，完成本題的解答．也可以選用其他的解題方案，此時不必填空，只需按照解答題的一般要求，進行解答．
如圖①，在一幅矩形地毯的四周鑲有寬度相同的花邊． 如圖②，地毯中央的矩形圖案長6米、寬3米，整個地毯的面積是40平方米，求花邊的寬．
精英家教網
（Ⅰ）設花邊的寬為x米，用含x的代數式表示：
矩形地毯ABCD的長為
 
米；
矩形地毯ABCD的寬為
 
米；
矩形地毯ABCD的面積為
 
米2；
（Ⅱ）列出方程，并求出問題的解．

查看答案和解析>>

科目：初中數學 來源： 題型：

九（1）班數學課題學習小組，為了研究學習二次函數問題，他們經歷了實踐——應用——探究的過程

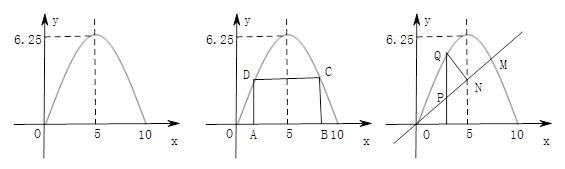
（1）實踐：他們對一條公路上橫截面為拋物線的單向雙車道的隧道進行測量，測得隧道的路面寬為10米，隧道頂部最高處距地面6.25米，并畫出了隧道截面圖，建立了如圖所示的直角坐標系，請你求出拋物線的解析式

（2）應用：按規定機動車輛通過隧道時，車頂部與隧道頂部在豎起方向上的高度差至少為0.5米，為了確保安全，問該隧道能否讓最寬3米，最高3.5米的兩輛車居中并列行駛（不考慮兩車之間的空隙）？

（3）探究：該課題學習小組為進一步探究拋物線的有關知識，他們借助上述拋物線模型，提出了以下兩個問題，請予解答：

①如圖，在拋物線內作矩形ABCD，使頂點C、D落在拋物線上，頂點A、B落在x軸上，設矩形ABCD的周長為為l，求l的最大值

②如圖，過原點作一條直線y=x，交拋物線于M，交拋物線的對稱軸于N，P為直線OM上一動點，過點P作x軸的垂線交拋物線于點Q，問在直線OM上是否存在點P，使以點P、N、Q為頂點的三角形為等腰直角三角形？若存在，求出點P的坐標，若不存在，請說明理由

 

 

 

 

 

 

 

 

 

查看答案和解析>>

科目：初中數學 來源： 題型：

九（1）班數學課題學習小組，為了研究學習二次函數問題，他們經歷了實踐——應用——探究的過程
（1）實踐：他們對一條公路上橫截面為拋物線的單向雙車道的隧道進行測量，測得隧道的路面寬為10米，隧道頂部最高處距地面6.25米，并畫出了隧道截面圖，建立了如圖所示的直角坐標系，請你求出拋物線的解析式
（2）應用：按規定機動車輛通過隧道時，車頂部與隧道頂部在豎起方向上的高度差至少為0.5米，為了確保安全，問該隧道能否讓最寬3米，最高3.5米的兩輛車居中并列行駛（不考慮兩車之間的空隙）？
（3）探究：該課題學習小組為進一步探究拋物線的有關知識，他們借助上述拋物線模型，提出了以下兩個問題，請予解答：
①如圖，在拋物線內作矩形ABCD，使頂點C、D落在拋物線上，頂點A、B落在x軸上，設矩形ABCD的周長為為l，求l的最大值
②如圖，過原點作一條直線y=x，交拋物線于M，交拋物線的對稱軸于N，P為直線OM上一動點，過點P作x軸的垂線交拋物線于點Q，問在直線OM上是否存在點P，使以點P、N、Q為頂點的三角形為等腰直角三角形？若存在，求出點P的坐標，若不存在，請說明理由
 

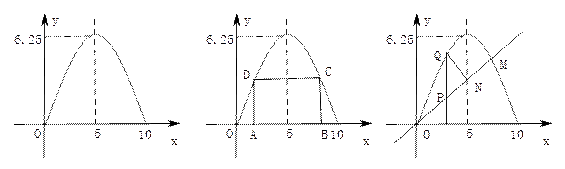查看答案和解析>>

科目：初中數學 來源：2013屆溫州平陽縣昆陽四中八年級下學期第一次月考考試數學卷 題型：選擇題

（本大題10分）（本大題有兩題，請同學們選擇你喜歡且拿手一題解答）

如圖，在△ABC中，AB=AC=13厘米，BC=10厘米，AD⊥BC于點D，動點P從點A出發以每秒1厘米的速度在線段AD上向終點D運動。設動點運動時間為t秒。

（1）求AD的長．（3分）

（2）當△PDC的面積為15平方厘米時，求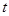的值．（4分）

（3）動點M從點C出發以每秒2厘米的速度在射線CB上運動．點M與點P同時出發，且當點P運動到終點D時，點M也停止運動。是否存在t，使得S△PMD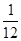＝S△ABC？若存在，請求出t的值；若不存在，請說明理由．（5分）

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

查看答案和解析>>

科目：初中數學 來源：2011年初中畢業升學考試（湖南岳陽卷）數學 題型：解答題

九（1）班數學課題學習小組，為了研究學習二次函數問題，他們經歷了實踐——應用——探究的過程

（1）實踐：他們對一條公路上橫截面為拋物線的單向雙車道的隧道進行測量，測得隧道的路面寬為10米，隧道頂部最高處距地面6.25米，并畫出了隧道截面圖，建立了如圖所示的直角坐標系，請你求出拋物線的解析式

（2）應用：按規定機動車輛通過隧道時，車頂部與隧道頂部在豎起方向上的高度差至少為0.5米，為了確保安全，問該隧道能否讓最寬3米，最高3.5米的兩輛車居中并列行駛（不考慮兩車之間的空隙）？

（3）探究：該課題學習小組為進一步探究拋物線的有關知識，他們借助上述拋物線模型，提出了以下兩個問題，請予解答：

①如圖，在拋物線內作矩形ABCD，使頂點C、D落在拋物線上，頂點A、B落在x軸上，設矩形ABCD的周長為為l，求l的最大值

②如圖，過原點作一條直線y=x，交拋物線于M，交拋物線的對稱軸于N，P為直線OM上一動點，過點P作x軸的垂線交拋物線于點Q，問在直線OM上是否存在點P，使以點P、N、Q為頂點的三角形為等腰直角三角形？若存在，求出點P的坐標，若不存在，請說明理由

 

 

 

 

 

 

 

 

 

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 亚洲精品一区久久久久久 | 真实国产露脸乱 | 欧美在线三级 | 在线观看91 | 精品不卡一区 | 日本一区二区精品 | 久久久久亚洲 | 国产精品一区99 | 欧美精品免费在线 | 日韩日韩日韩日韩日韩日韩日韩 | 日韩免费视频一区二区 | 日韩精品| 久久国产精品一区二区 | 91午夜在线 | 成人三级黄色 | 精品一二区 | 成人欧美一区二区三区 | a√天堂资源在线 | 久久成人国产 | 成人三区| 污网址在线观看 | а天堂中文最新一区二区三区 | 亚洲欧美日韩高清 | 亚洲日本乱码一区二区三区 | 欧美多人在线 | 久色成人 | 中字一区| 在线亚洲激情 | 99精品国产一区二区三区 | heyzo在线观看 | 国产精品国产自产拍高清 | 国产在线看片 | 欧美日本在线播放 | 欧美在线 | 午夜精品久久久久久久白皮肤 | 国产福利电影一区 | 二区在线视频 | 久久91精品国产91久久跳 | 午夜99 | 国产一区二区三区色淫影院 | 午夜在线 |