【題目】“三角形的一個外角等于與它不相鄰的兩個內角的和”揭示了三角形的一個外角與它的兩個內角之間的數量關系，請探索并寫出三角形沒有公共頂點的兩個外角與它的第三個內角之間的關系：_______.
手拉手全優練考卷系列答案科目：初中數學 來源： 題型：
【題目】某車站在春運期間為改進服務,抽查了100名旅客從開始在窗口排隊到購到車票所用時間t(以下簡稱購票用時,單位:分),得到如下表所示的頻數分布表.
分組 | 頻數 | |
一組 | 0≤t<5 | 0 |
二組 | 5≤t<10 | 10 |
三組 | 10≤t<15 | 10 |
四組 | 15≤t<20 | |
五組 | 20≤t<25 | 30 |
合計 | 100 | |
(1)在表中填寫缺失的數據;
(2)畫出頻數分布直方圖;
(3)旅客購票用時的平均數可能落在哪一小組內?
(4)若每增加一個購票窗口可以使平均購票用時降低5分,要使平均購票用時不超過10分,那么請你決策一下至少要增加幾個窗口?
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】甲、乙兩班舉行電腦漢字輸入比賽，各選10名選手參賽，各班參賽學生每分鐘輸入漢字個數統計如下表：
輸入漢字個數（個） | 132 | 133 | 134 | 135 | 136 | 137 | ||
甲班人數人） | 1 | 0 | 2 | 4 | 1 | 2 | ||
乙班人數（人） | 0 | 1 | 4 | 1 | 2 | 2 | ||
請分別判斷下列同學是說法是否正確，并說明理由．
（1）兩個班級輸入漢字個數的平均數相同；
（2）兩個班學生輸入漢字的中位數相同眾數也相同；
（3）甲班學生比乙班學生的成績穩定．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某次考試中，某班級的數學成績統計圖如圖.下列說法錯誤的是( )
A. 得分在70～80分之間的人數最多 B. 該班的總人數為40
C. 得分在90～100分之間的人數最少 D. 及格(≥60分)人數是26
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】2017年3月全國兩會勝利召開，某學校就兩會期間出現頻率最高的熱詞：A．藍天保衛戰，B．不動產保護，C．經濟增速，D．簡政放權等進行了抽樣調查，每個同學只能從中選擇一個“我最關注”的熱詞，如圖是根據調查結果繪制的兩幅不完整的統計圖．請你根據統計圖提供的信息，解答下列問題：
（1）本次調查中，一共調查了 名同學；
（2）條形統計圖中，m= ，n= ；
（3）從該校學生中隨機抽取一個最關注熱詞D的學生的概率是多少？
【答案】（1）300；（2）60，90；（3）從該校學生中隨機抽取一個最關注熱詞D的學生的概率是
．
【解析】試題分析：（1）根據A的人數為105人，所占的百分比為35%，求出總人數，即可解答；
（2）C所對應的人數為：總人數×30%，B所對應的人數為：總人數﹣A所對應的人數﹣C所對應的人數﹣D所對應的人數，即可解答；
（3）根據概率公式，即可解答．
試題解析：（1）105÷35%=300（人），
故答案為：300；
（2）n=300×30%=90（人），
m=300﹣105﹣90﹣45=60（人）．
故答案為：60，90；
（3）從該校學生中隨機抽取一個最關注熱詞D的學生的概率是
=
，
答：從該校學生中隨機抽取一個最關注熱詞D的學生的概率是
．
【題型】解答題
【結束】
26
【題目】已知正方形ABCD的邊長為8，點E為BC的中點，連接AE，并延長交射線DC于點F，將△ABE沿著直線AE翻折，點B落在B′處，延長AB′，交直線CD于點M．
（1）判斷△AMF的形狀并證明；
（2）將正方形變為矩形ABCD，且AB=6，BC=8，若B′恰好落在對角線AC上時，得到圖2，此時CF=_____， 
=_____；
（3）在（2）的條件下，點E在BC邊上．設BE為x，△ABE沿直線AE翻折后與矩形ABCD重合的面積為y，求y與x之間的函數關系式．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知二次函數y=x2-2x-3.
（1）求函數圖象的頂點坐標，與x軸和y軸的交點坐標，并畫出函數的大致圖象；
（2）根據圖象直接回答：當x滿足 時，y＜0；當-1＜x＜2時，y的范圍是 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，PQ∥MN，A、B分別為直線MN、PQ上兩點，且∠BAN＝45°，若射線AM繞點A順時針旋轉至AN后立即回轉，射線BQ繞點B逆時針旋轉至BP后立即回轉，兩射線分別繞點A、點B不停地旋轉，若射線AM轉動的速度是a°/秒，射線BQ轉動的速度是b°/秒，且a、b滿足|a﹣5|+（b﹣1）2＝0．（友情提醒：鐘表指針走動的方向為順時針方向）
（1）a＝ ，b＝ ；
（2）若射線AM、射線BQ同時旋轉，問至少旋轉多少秒時，射線AM、射線BQ互相垂直．
（3）若射線AM繞點A順時針先轉動18秒，射線BQ才開始繞點B逆時針旋轉，在射線BQ到達BA之前，問射線AM再轉動多少秒時，射線AM、射線BQ互相平行？
查看答案和解析>>
科目：初中數學 來源： 題型：
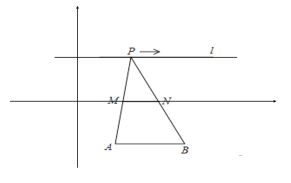
【題目】如圖，在直角坐標系中，點
，
為定點，A（2，－3），B（4，－3），定直線
，
是
上一動點，到AB的距離為6，
，
分別為
，
的中點，對下列各值：①線段
的長度始終為1；②
的周長固定不變；③
的面積固定不變；④若存在點Q使得四邊形APBQ是平行四邊形，則Q到所在的直線的距離必為9；其中說法正確的是__（填序號）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
