
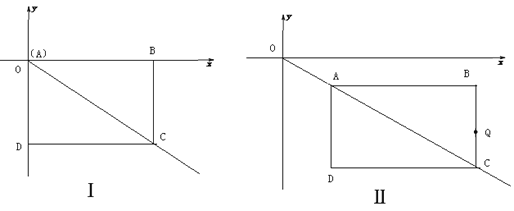
【題目】如圖Ⅰ,在第四象限的矩形ABCD,點A與坐標原點O重合,且AB=4,AD=3.如圖Ⅱ,矩形ABCD沿OC方向以每秒1個單位長度的速度運動,同時點Q從B點出發也以每秒1個單位長度的速度沿矩形ABCD的邊BC經過點C向點D運動,當點Q到達點D時,矩形ABCD和點Q同時停止運動,設點Q運動的時間為t秒.
(1)在圖Ⅰ中,點C的坐標(____),在圖Ⅱ中,當t=2時,點A坐標(______),Q坐標(______)
(2)當點Q在線段BC或線段CD上運動時,求出△ACQ的面積S關于t的函數關系式,并寫出t的取值范圍;
(3)點Q在線段BC或線段CD上運動時,作QM⊥x軸,垂足為點M,當△QMO與△ACD相似時,求出相應的t值.
【答案】(1)C(4,-3); A(![]() ), Q(
), Q(![]() );
);
(2)①當Q在BC上,即0≤t≤3時,S=6-2t,②當Q在CD上,即3<t≤7時,S=![]() ;
;
(3)當t=3時,△QMO與△ACD相似.
【解析】試題分析:(1)根據AB=4,AD=3,可得點A的坐標,過A作AE⊥x軸于E,根據△AOE∽△CAB,可得AE:OE:AO=3:4:5,再根據當t=2時,OA=2,OE=![]() ,AE=
,AE=![]() ,BQ=2,可得點A和點Q的坐標;(2)分兩種情況進行討論:①當點Q在BC上時,②當點Q在CD上時,分別根據△ACQ的面積計算方法,求得S關于t的函數關系式,并根據點Q的位置寫出t的取值范圍;(3)先過A作AE⊥x軸于E,根據△AOE∽△CAB,得出AE:OE:AO=3:4:5,再根據OA=t,得出OE=
,BQ=2,可得點A和點Q的坐標;(2)分兩種情況進行討論:①當點Q在BC上時,②當點Q在CD上時,分別根據△ACQ的面積計算方法,求得S關于t的函數關系式,并根據點Q的位置寫出t的取值范圍;(3)先過A作AE⊥x軸于E,根據△AOE∽△CAB,得出AE:OE:AO=3:4:5,再根據OA=t,得出OE=![]() t,AE=
t,AE=![]() t,再分兩種情況進行討論:①當點Q在BC上時,連接OQ,②當點Q在CD上時,連接OQ,分別根據相似三角形的對應邊成比例,列出關于t的比例式,求得t的值并檢驗即可.
t,再分兩種情況進行討論:①當點Q在BC上時,連接OQ,②當點Q在CD上時,連接OQ,分別根據相似三角形的對應邊成比例,列出關于t的比例式,求得t的值并檢驗即可.
試題解析: (1)如圖所示,
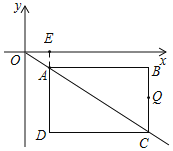
∵AB=4,AD=3,
∴A(4,3),AC=5,
過A作AE⊥x軸于E,則△AOE∽△CAB,
∴AE:OE:AO=3:4:5,
當t=2時,OA=2,OE=85,AE=65,BQ=2,
∴A(![]() ,
,![]() ),
),
∵OE+AB=![]() ,AE+BQ=
,AE+BQ=![]() ,
,
∴Q(![]() ,
,![]() ),
),
故答案為:(4,3),(![]() ,
,![]() ),(
),(![]() ,
, ![]() );
);
(2)①當點Q在BC上時,連接AQ,
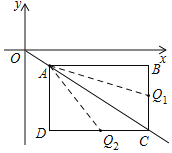
∵BQ=t,BC=3,
∴CQ=3t,
∴△ACQ的面積=![]() ×CQ×AB,即S=
×CQ×AB,即S=![]() ×(3t)×4=2t+6(0t<3);
×(3t)×4=2t+6(0t<3);
②當點Q在CD上時,連接AQ,
∵QC+BC=t,BC=3,
∴CQ=t3,
∴△ACQ的面積=![]() ×CQ×AD,即S=
×CQ×AD,即S=![]() ×(t3)×3=
×(t3)×3=![]() t
t![]() (3t7);
(3t7);
∴S關于t的函數關系式為S=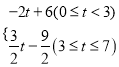 ;
;
(3)如圖所示,過A作AE⊥x軸于E,則△AOE∽△CAB,
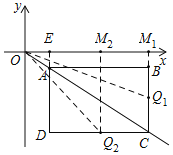
∴AE:OE:AO=3:4:5,
∵OA=t,
∴OE=![]() t,AE=
t,AE=![]() t,
t,
①當點Q在BC上時,連接OQ,
∵∠OMQ=∠D=90°,而BQ=t,
∴當![]() 時,△OMQ∽△CDA,
時,△OMQ∽△CDA,
此時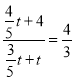 ,解得t=3;
,解得t=3;
當![]() 時,△OMQ∽△ADC,
時,△OMQ∽△ADC,
此時, 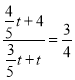 ,解得t=10>3,(舍去);
,解得t=10>3,(舍去);
②當點Q在CD上時,連接OQ,而DQ=3+4t=7t=EM,
∴OM=![]() t+7t=7
t+7t=7![]() t,
t,
∴當![]() 時,△OMQ∽△CDA,
時,△OMQ∽△CDA,
此時, 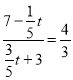 ,解得t=3;
,解得t=3;
當![]() 時,△OMQ∽△ADC,
時,△OMQ∽△ADC,
此時, 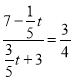 解得t=
解得t=![]() >7,(舍去)
>7,(舍去)
綜上所述,當△QMO與△ACD相似時,t的值為3秒。


 應用題作業本系列答案
應用題作業本系列答案科目:初中數學 來源: 題型:
【題目】有一列按一定順序和規律排列的數:
第一個數是![]() ;
;
第二個數是![]() ;
;
第三個數是![]() ;
;
…
對任何正整數n,第n個數與第(n+1)個數的和等于![]() .
.
(1)經過探究,我們發現:![]()
![]()
![]()
設這列數的第5個數為a,那么![]() ,
,![]() ,
,![]() ,哪個正確?
,哪個正確?
請你直接寫出正確的結論;
(2)請你觀察第1個數、第2個數、第3個數,猜想這列數的第n個數(即用正整數n表示第n數),并且證明你的猜想滿足“第n個數與第(n+1)個數的和等于![]() ”;
”;
(3)設M表示![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,這2016個數的和,即
,這2016個數的和,即![]() ,
,
求證:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用四舍五人法按要求把2.05446取近似值,其中錯誤的是( )
A.2.1(精確到0.1)
B.2.05(精確到百分位)
C.2.054(精確到0.001)
D.2.0544(精確到萬分位)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校開展課外體育活動,決定開展:籃球、乒乓球、踢毽子、跑步四種活動項目.為了解學生最喜歡哪一種活動項目(每人只選取一種).隨機抽取了部分學生進行調查,并將調查結果繪成如下統計圖,請你結合圖中信息解答下列問題.
(1)樣本中最喜歡籃球項目的人數所占的百分比為 ,其所在扇形統計圖中對應的圓心角度數是 度;
(2)請把條形統計圖補充完整;
(3)若該校有學生1000人,請根據樣本估計全校最喜歡踢毽子的學生人數約是多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線y=![]() 與x軸、y軸分別交于A,B兩點,Q是直線AB上一動點,⊙Q的半徑為1.當⊙Q與坐標軸相切時,點Q的坐標為____________.
與x軸、y軸分別交于A,B兩點,Q是直線AB上一動點,⊙Q的半徑為1.當⊙Q與坐標軸相切時,點Q的坐標為____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一跨河橋,橋拱是圓弧形,跨度(AB)為12米,拱高(CN)為2米,求:
(1)橋拱半徑;
(2)大雨過后,橋下河面寬度(DE)為10米,求水面漲高了多少?
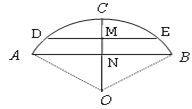
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】古希臘著名的畢達哥拉斯學派把1、3、6、10…這樣的數稱為“三角形數”,而把l、4、9、16…這樣的數稱為“正方形數”.從圖中可以發現,任何一個大于1的正方形數”都可以看作兩個相鄰“三角形數”之和.下列等式中。符合這一規律的是( )

A. 15=4+11 B. 25=9+16
C. 49=21+28 D. 61=25+36
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙、丙三人拿出同樣多的錢,合伙訂購同種規格的若干件商品.商品買來后,甲、乙分別比丙多拿了12、9件商品,最后結算時,乙付給丙20元,那么,甲應付給丙元.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com