
【題目】如圖,拋物線![]() 與
與![]() 軸交于
軸交于![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,且
,且![]() ,
,![]() .
.
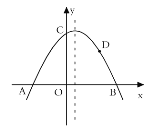
(1)求拋物線的表達式;
(2)點![]() 是拋物線上一點.
是拋物線上一點.
①在拋物線的對稱軸上,求作一點![]() ,使得
,使得![]() 的周長最小,并寫出點
的周長最小,并寫出點![]() 的坐標;
的坐標;
②連接![]() 并延長,過拋物線上一點
并延長,過拋物線上一點![]() (點
(點![]() 不與點
不與點![]() 重合)作
重合)作![]() 軸,垂足為
軸,垂足為![]() ,與射線
,與射線![]() 交于點
交于點![]() ,是否存在這樣的點
,是否存在這樣的點![]() ,使得
,使得![]() ,若存在,求出點
,若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
【答案】(1)![]() ;(2)①連接
;(2)①連接![]() 交拋物線對稱軸于點
交拋物線對稱軸于點![]() ,則點
,則點![]() 即為所求,點
即為所求,點![]() 的坐標為
的坐標為![]() ;②存在;點
;②存在;點![]() 的坐標為
的坐標為![]() 或
或![]() .
.
【解析】
(1)由![]() ,
,![]() 得到A(-2,0),C(3,0),即可寫出拋物線的交點式.
得到A(-2,0),C(3,0),即可寫出拋物線的交點式.
(2)①因為![]() 關于對稱軸對稱,所以
關于對稱軸對稱,所以![]() ,由兩點之間線段最短,知連接
,由兩點之間線段最短,知連接![]() 交拋物線對稱軸于點
交拋物線對稱軸于點![]() ,則點
,則點![]() 即為所求,先用待定系數法求出
即為所求,先用待定系數法求出![]() 解析式,將對稱軸代入得到
解析式,將對稱軸代入得到![]() 點坐標.
點坐標.
②設點![]() ,根據拋物線的解析式、直線
,根據拋物線的解析式、直線![]() 的解析式,寫出Q、M的坐標,分當
的解析式,寫出Q、M的坐標,分當![]() 在
在![]() 上方、下方兩種情況,列關于m的方程,解出并取大于-2的解,即可寫出
上方、下方兩種情況,列關于m的方程,解出并取大于-2的解,即可寫出![]() 的坐標.
的坐標.
(1)∵![]() ,
,![]() ,
,
結合圖象,得A(-2,0),C(3,0),
∴拋物線![]() 可表示為:
可表示為:![]() ,
,
∴拋物線的表達式為![]() ;
;
(2)①∵![]() 關于對稱軸對稱,
關于對稱軸對稱,
∴![]() ,
,
∴連接![]() 交拋物線對稱軸于點
交拋物線對稱軸于點![]() ,則點
,則點![]() 即為所求.
即為所求.
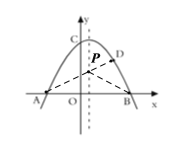
將點![]() ,
,![]() 的坐標代入一次函數表達式
的坐標代入一次函數表達式![]() ,
,
得直線![]() 的函數表達式為
的函數表達式為![]() .
.
拋物線的對稱軸為直線![]() ,
,
當![]() 時,
時,![]() ,
,
故點![]() 的坐標為
的坐標為![]() ;
;
②存在;設點![]() ,則
,則![]() ,
,![]() .
.
當![]() 在
在![]() 上方時,
上方時,
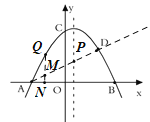
![]() ,
,![]() ,
,![]() ,解得
,解得![]() (舍)或
(舍)或![]() ;
;
當![]() 在
在![]() 下方時,
下方時,
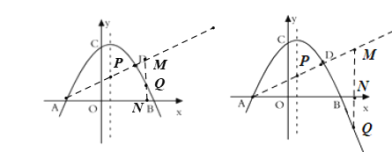
![]() ,
,![]() ,
,![]() ,解得
,解得![]() (舍)或
(舍)或![]() ,
,
綜上所述,![]() 的值為
的值為![]() 或5,
或5,
![]() 點
點![]() 的坐標為
的坐標為![]() 或
或![]() .
.


科目:初中數學 來源: 題型:
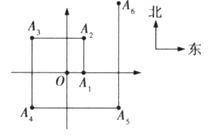
【題目】如圖,一個機器人從點O出發,向正東方向走3m到達點![]() ,再向正北方向走6m到達點
,再向正北方向走6m到達點![]() ,再向正西方向走9m到達點
,再向正西方向走9m到達點![]() ,再向正南方向走12m到達點
,再向正南方向走12m到達點![]() ,再向正東方向走15m到達點
,再向正東方向走15m到達點![]() ,按如此規律走下去,當機器人走到點
,按如此規律走下去,當機器人走到點![]() 時,點
時,點![]() 的坐標是________.
的坐標是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2020年2月22日深圳地鐵10號線華南城站試運行,預計今年6月正式開通.在地鐵的建設中,某段軌道的鋪設若由甲乙兩工程隊合做,12天可以完成,共需工程費用27720元;已知乙隊單獨完成這項工程所需時間是甲隊單獨完成這項工程所需時間的1.5倍,且甲隊每天的工程費用比乙隊多250元.
(1)求甲、乙兩隊單獨完成這項工程各需多少天?
(2)若工程管理部門決定從這兩個隊中選一個隊單獨完成此項工程,從節約資金的角度考慮,應選擇哪個工程隊?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
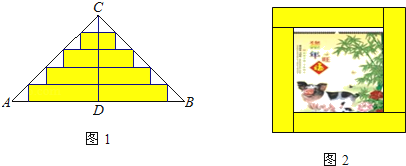
【題目】如圖1,△ABC是一張等腰直角三角形彩色紙,AC=BC,將斜邊上的高CD五等分,然后裁出4張寬度相等的長方形紙條.若用這4張紙條剛好可以為一幅正方形美術作品鑲邊(紙條不重疊),如圖2,則正方形美術作品與鑲邊后的作品的面積之比為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
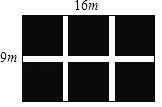
【題目】如圖,某小區在一塊長為16m,寬為9m的矩形空地上新修三條寬度相同的小路,其中一條和矩形的一邊平行,另外兩條和矩形的另一邊平行,空地剩下的部分種植花草,使得花草區域占地面積為120m2.設小路的寬度為xm,則下列方程:
①(16﹣2x)(9﹣x)=120
②16×9﹣9×2x﹣(16﹣2x)x=120
③16×9﹣9×2x﹣16x+x2=120,
其中正確的是( )
A.①B.②C.①②D.①②③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=![]() ,AD=3,點E從點B出發,沿BC邊運動到點C,連結DE,點E作DE的垂線交AB于點F.在點E的運動過程中,以EF為邊,在EF上方作等邊△EFG,則邊EG的中點H所經過的路徑長是( )
,AD=3,點E從點B出發,沿BC邊運動到點C,連結DE,點E作DE的垂線交AB于點F.在點E的運動過程中,以EF為邊,在EF上方作等邊△EFG,則邊EG的中點H所經過的路徑長是( )

A. 2 ![]() B. 3
B. 3![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
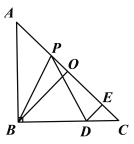
【題目】如圖所示,在等腰直角三角形ABC中,O是斜邊AC的中點,P是斜邊AC上的一個動點,D為BC上的一點,且PB=PD,DE⊥AC,垂足為點E,求證:PE=BO
查看答案和解析>>
科目:初中數學 來源: 題型:
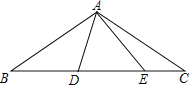
【題目】如圖,在△ABC中,AB=AC=2![]() ,∠BAC=120°,點D、E都在邊BC上,∠DAE=60°.若BD=2CE,則DE的長為________.
,∠BAC=120°,點D、E都在邊BC上,∠DAE=60°.若BD=2CE,則DE的長為________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com