
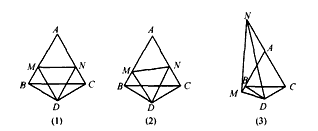
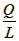 =____;
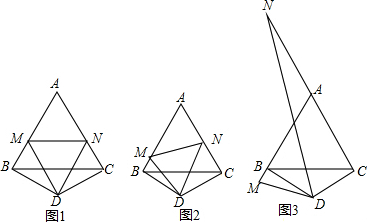
=____; 解:(1)BM、NC、MN之間的數量關系BM+NC=MN,此時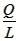 = = ; ; |
|
| (2)猜想:結論仍然成立, 證明:如圖,延長AC至E,使CE=BM,連接DE, ∵BD=CD,且∠BDC=120°, ∴∠DBC=∠DCB=30°, 又△ABC是等邊三角形, ∴∠MBD=∠NCD=90°, 在△MBD與△ECD中, BM=CE,∠MBD=∠ECD,BD=DC, ∴△MBD≌△ECD(SAS), ∴DM=DE,∠BDM=∠CDE, ∴∠EDN=∠BDC-∠MDN=60°, 在△MDN與△EDN中: DM=DE,∠MDN=∠EDN,DN=DN, ∴△MDN≌△EDN(SAS), ∴MN=NE=NC+BM, △AMN 的周長Q=AM+AN+MN =AM+AN+(NC+BM) =(AM+BM)+(AN+NC) =AB+AC =2AB, 而等邊△ABC的周長L=3AB, ∴ 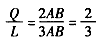 ; ; |
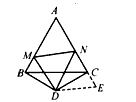 |
| (3)當M、N分別在AB、CA的延長線上時, 若AN=x,則Q=2x+ 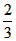 L(用x、L表示)。 L(用x、L表示)。 |


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
| Q | L |
查看答案和解析>>
科目:初中數學 來源: 題型:
| Q | L |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

 =______;
=______;查看答案和解析>>
科目:初中數學 來源:初三數學圓及旋轉題庫 第2講:旋轉的應用(解析版) 題型:解答題

 =______;
=______;查看答案和解析>>
科目:初中數學 來源:2009年北京市崇文區中考數學一模試卷(解析版) 題型:解答題
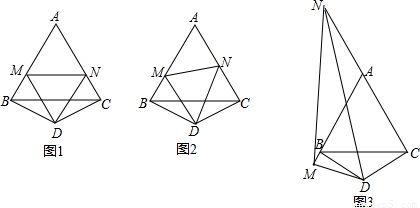
 =______;
=______;查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com