(2005•泉州質檢)某公園出售的一次性使用門票,每張10元,同時又推出購買“個人年票”的售票方法(從購買日起,可供持票者使用一年),年票分A,B兩類:A類年票每張100元,持票者每次進入公園無需再購買門票,B類年票每張40元,持票者每次進入公園時需再購買每次2元的門票.現有甲,乙,丙三位游客在一年中分別選擇用A類年票,B類年票,一次性使用門票三種方式去游園,并且乙,丙每人一年中恰好都進入該公園x次.
(1)請分別寫出乙,丙每人一年的門票費支出(用含x的代數式表示);
(2)①在三位游客每人一年的門票費支出中,當甲的支出為最少時:乙,丙每人一年中進入該公園至少超過多少次?
②求此時三位游客一年中游園共支出的門票費總額的最小值.
【答案】
分析:(1)根據題意直接列式即可;
(2)根據“乙一年的門票支出大于100”“丙一年的門票支出大于100”列不等式求解即可得x的范圍;設此時三游客一年中游園共支出的門票總額為W元,則W可以表示成x的函數,根據函數的性質,就可以求出.
解答:解:(1)乙一年的門票支出為(40+20x)元(2分)
丙一年的門票支出為10x元(4分).
(2)①依題意得
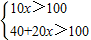
(6分)
解得:x>30 (7分)
則乙丙兩人一年中進入該公園至少超過30次(8分)
②設此時三位游客一年中游園共支出的門票總額為W元
則W=100+40+2x+10x
=12x+140(x>30,且x為正整數) (10分)
∵w隨x的增大而增大(11分)
∴當x=31時
w的最小值為12×31+140=512元
∴此時三位游客一年中游園共支出的門票費的最小值為512元(13分)
點評:本題考查一元一次不等式組的應用,將現實生活中的事件與數學思想聯系起來,讀懂題列出不等式關系式即可求解.要會根據自變量的取值范圍結合函數的單調性求函數的最值問題.

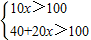 (6分)
(6分)

 .
.