
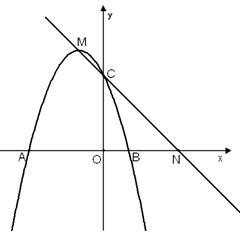
已知拋物線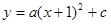 與
與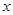 軸交于點A(
軸交于點A(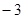 ,0),
,0),
(1)直接寫出拋物線與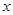 軸的另一個交點B的坐標;
軸的另一個交點B的坐標;
(2)若直線過拋物線頂點M及拋物線與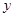 軸的交點
軸的交點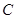 (0,3).
(0,3).
① 求直線MC所對應的函數關系式;
② 若直線MC與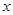 軸的交點為
軸的交點為 ,在拋物線上是否存在點
,在拋物線上是否存在點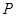 ,使得△NPC是以NC為直角邊的直角三角形?若存在,求出點
,使得△NPC是以NC為直角邊的直角三角形?若存在,求出點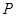 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
(1)B(1,0)(2)①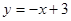 ②
②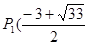 ,
,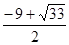 ),
),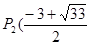 ,
, ),
),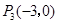
【解析】解:(1)B(1,0)................(3分)
(2)①∵點B(1,0),C(0,3)在拋物線上,拋物線與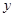 軸交于點C(0,3).
軸交于點C(0,3).
∴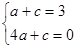 解得
解得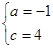 ∴拋物線所對應的函數關系式為
∴拋物線所對應的函數關系式為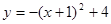 .....(5分)
.....(5分)
∴M(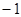 ,4)設直線MC所對應的函數關系式為
,4)設直線MC所對應的函數關系式為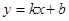 ,
,
∴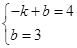 ,解得
,解得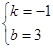 ,∴直線MC所對應的函數關系式為
,∴直線MC所對應的函數關系式為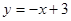 .....(7分)
.....(7分)
②假設在拋物線上存在異于點C的點P,使得△NPC是以NC為直角邊的直角三角形.
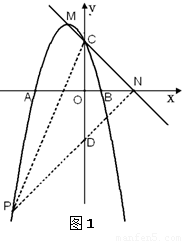
①若PN為△NPC的另一條直角邊,如圖1.
易得直線MC與x軸的交點坐標為N(3,0).
∵OC=ON,,∴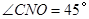 ,
,
在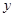 軸上取點D(0,
軸上取點D(0,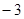 ),連結ND交拋物線于點P.
),連結ND交拋物線于點P.
∵ON=OD,∴ .∴
.∴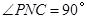 .
.
設直線ND的函數表達式為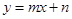 .
.
可得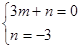 ,解得
,解得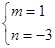
∴直線ND的函數表達式為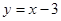 .....(9分)
.....(9分)
設點P(x,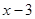 ),并將它代入拋物線的函數表達式,得
),并將它代入拋物線的函數表達式,得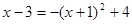
即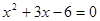 .解得
.解得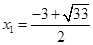 ,
,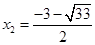
∴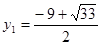 ,
,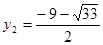
∴滿足條件的點為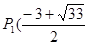 ,
,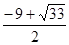 ),....(10分)
),....(10分)
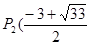 ,
, ).
).
②若PC是另一條直角邊,如圖2.
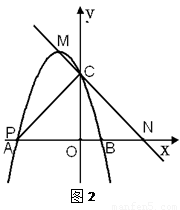
∵點A是拋物線與x軸的另一交點,
∴點A的坐標為(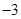 ,0).
,0).
連結AC.∵OA=OC,∴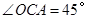 .又
.又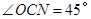 ,
,
∴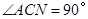 ,∴點A就是所求的點
,∴點A就是所求的點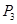 (
(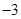 ,0). ....(12分)
,0). ....(12分)
[或:求出直線AC的函數表達式為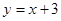 .設點P(x,
.設點P(x,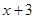 ),代入拋物線 的函數表達式,得
),代入拋物線 的函數表達式,得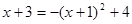 ,即
,即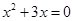 .解得
.解得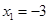 ,
,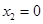 . ∴
. ∴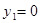 ,
,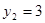 ,∴點
,∴點 ,
,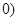 ,
,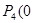 ,
, (舍去).]
(舍去).]
綜上可知,在拋物線上存在滿足條件的點有3個,分別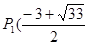 ,
,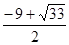 ),
),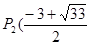 ,
, ),
),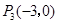 .....(13分)
.....(13分)
(1)根據已知拋物線的解析式,可得到拋物線的對稱軸方程,從而根據A點坐標求出點B的坐標.
(2)根據A、B、C三點坐標,即可求得拋物線的解析式和它的頂點坐標;
①已經求得M、C的坐標,利用待定系數法求解即可;
②假設存在符合條件的P點,分兩種情況考慮:
1)以N為直角頂點,即PN為另一條直角邊;
易求得點N的坐標,根據C、N點的坐標可知∠CNO=45°,若∠PNC=90°,可在y軸截取OD=ON,易得點D的坐標,即可求出直線DN的解析式,聯立拋物線的解析式即可得到點P的坐標;
2)以C為直角頂點,即PC為另一條直角邊;
根據A、C的縱坐標知:∠CAN=45°,此時∠ACN=90°,那么點A即為所求的P點;
綜合上述兩種情況,即可得到符合條件的P點坐標.


科目:初中數學 來源: 題型:
在平面直角坐標系中,已知拋物線![]() 與
與![]() 軸交于點
軸交于點![]() 、
、![]() (點
(點![]() 在點
在點![]() 的左側),與
的左側),與![]() 軸的正半軸交于點
軸的正半軸交于點![]() ,頂點為
,頂點為![]() .
.
(Ⅰ)若![]() ,
,![]() ,求此時拋物線頂點
,求此時拋物線頂點![]() 的坐標;
的坐標;
(Ⅱ)將(Ⅰ)中的拋物線向下平移,若平移后,在四邊形ABEC中滿足
S△BCE = S△ABC,求此時直線![]() 的解析式;
的解析式;
(Ⅲ)將(Ⅰ)中的拋物線作適當的平移,若平移后,在四邊形ABEC中滿足
S△BCE = 2S△AOC,且頂點![]() 恰好落在直線
恰好落在直線![]() 上,求此時拋物線的解析式.
上,求此時拋物線的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
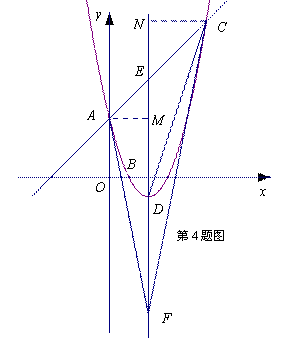
如圖,已知拋物線與![]() 軸交于點
軸交于點![]() ,
,![]() ,與y軸交于點
,與y軸交于點![]() .
.

(1)求拋物線的解析式及其頂點D的坐標;
(2)設直線CD交![]() 軸于點E.在線段OB的垂直平分線上是否存在點P,使得點P到直線CD的距離等于點P到原點O的距離?如果存在,求出點P的坐標;如果不存在,請說明理由
軸于點E.在線段OB的垂直平分線上是否存在點P,使得點P到直線CD的距離等于點P到原點O的距離?如果存在,求出點P的坐標;如果不存在,請說明理由
查看答案和解析>>
科目:初中數學 來源: 題型:
 與
與 軸交于點
軸交于點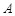 (-1,0)、
(-1,0)、 (3,0),與
(3,0),與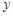 軸的正半軸交于點
軸的正半軸交于點 ,頂點為
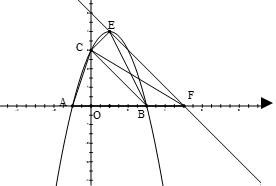
,頂點為 .
.
 的坐標;
的坐標; 軸于點F,在不添加線和字母情況下,圖中面積相等的三角形有: .
軸于點F,在不添加線和字母情況下,圖中面積相等的三角形有: . 軸交于點M、N,與
軸交于點M、N,與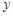 軸的正半軸交于點P,頂點為Q.在四邊形MNQP中滿足S△NPQ = S△MNP,求此時直線PN的解析式
軸的正半軸交于點P,頂點為Q.在四邊形MNQP中滿足S△NPQ = S△MNP,求此時直線PN的解析式查看答案和解析>>
科目:初中數學 來源: 題型:
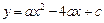 與
與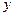 軸交于點
軸交于點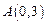 ,點
,點 是拋物線上的點,且滿足
是拋物線上的點,且滿足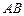 ∥
∥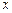 軸,點
軸,點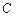 是拋物線的頂點.
是拋物線的頂點.
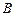 點坐標;
點坐標;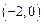 ,求拋物線的表達式;
,求拋物線的表達式;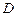 在線段
在線段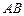 上,若以點
上,若以點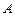 、
、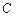 、
、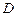 為頂點的三角形與
為頂點的三角形與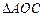 相似,試求點
相似,試求點 的坐標.
的坐標.查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,已知拋物線![]() 與
與![]() 軸交于點
軸交于點![]() ,且經過
,且經過![]() 兩點,點
兩點,點![]() 是拋物線頂點,
是拋物線頂點,![]() 是對稱軸與直線
是對稱軸與直線![]() 的交點,
的交點,![]() 與
與![]() 關于點
關于點![]() 對稱.
對稱.
(1)求拋物線的解析式;
(2)求證:![]() ;
;
(3)在拋物線的對稱軸上是否存在點![]() ,使
,使![]() 與
與![]() 相似.若有,請求出所有符合條件的點
相似.若有,請求出所有符合條件的點![]() 的坐標;若沒有,請說明理由.
的坐標;若沒有,請說明理由.
 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com