
【題目】如圖,已知△ABC三個頂點的坐標分別為(1,2),(-2,3),(-1,0),把它們的橫坐標和縱坐標都擴大到原來的2倍,得到點 ![]() ,
, ![]() ,
, ![]() .下列說法正確的是( )
.下列說法正確的是( ) 
A.△ ![]() 與△ABC是位似圖形,位似中心是點(1,0)
與△ABC是位似圖形,位似中心是點(1,0)
B.△ ![]() 與△ABC是位似圖形,位似中心是點(0,0)
與△ABC是位似圖形,位似中心是點(0,0)
C.△ ![]() 與△ABC是相似圖形,但不是位似圖形
與△ABC是相似圖形,但不是位似圖形
D.△ ![]() 與△ABC不是相似圖形
與△ABC不是相似圖形
【答案】B
【解析】解答:∵△ABC三個頂點的坐標分別為(1,2),(-2,3),(-1,0),把它們的橫坐標和縱坐標都擴大到原來的2倍 ∴點 ![]() ,
, ![]() ,
, ![]() 的坐標分別為(2,4),(-4,6),(-2,0)
的坐標分別為(2,4),(-4,6),(-2,0)
∴直線AA′,BB′,CC′得解析式分別為y=2x , y=- ![]() x , y=0
x , y=0
∴對應點的連線交于原點
∴△ ![]() 與△ABC是位似圖形,位似中心是點(0,0)
與△ABC是位似圖形,位似中心是點(0,0)
故選:B.
分析:由已知條件△ABC三個頂點的坐標分別為(1,2),(-2,3),(-1,0),把它們的橫坐標和縱坐標都擴大到原來的2倍,求得直線AA′,BB′,CC′得解析式分別為y=2x , y=- ![]() x , y=0,可知△
x , y=0,可知△ ![]() 與△ABC是位似圖形,位似中心是點(0,0).此題考查了位似的相關知識,位似是相似的特殊形式,位似圖形的對應點的連線交于一點.
與△ABC是位似圖形,位似中心是點(0,0).此題考查了位似的相關知識,位似是相似的特殊形式,位似圖形的對應點的連線交于一點.
【考點精析】掌握位似變換是解答本題的根本,需要知道它們具有相似圖形的性質外還有圖形的位置關系(每組對應點所在的直線都經過同一個點—位似中心).


科目:初中數學 來源: 題型:
【題目】如圖,已知四點A,B,C,D,用圓規和無刻度的直尺按下列要求與步驟畫出圖形并計算:

(1)畫直線AB;
(2)畫射線DC;
(3)延長線段DA至點E,使AE=AB;(保留作圖痕跡)
(4)畫一點P,使點P既在直線AB上,又在線段CE上;
(5)若AB=2cm,AD=1cm,求線段DE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形 ABCD 中,點 E 是對角線 BD 上一動點,AE 的延長線交 CD 于點 F,交 BC 的延長線于點 G,M 是 FG 的中點.
(1)求證: ∠DAE=∠DCE;
(2)判斷線段 CE 與 CM 的位置關系,并證明你的結論;
(3)當![]() ,并且
,并且![]() 恰好是等腰三角形時,求 DE 的長.
恰好是等腰三角形時,求 DE 的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】設實數a,b,c滿足a>b>c(ac<0),且|c|<|b|<|a|,則|x-a|+|x+b|+|x-c|的最小值為( )
A. ![]() B. |b| C. a+b D. -c-a
B. |b| C. a+b D. -c-a
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知含字母m,n的代數式是:![]() .
.
(1)化簡這個代數式.
(2)小明取m,n互為倒數的一對數值代入化簡的代數式中,恰好計算得代數式的值等于0.那么小明所取的字母n的值等于多少?
(3)聰明的小智從化簡的代數式中發現,只要字母n取一個固定的數,無論字母m取何數,代數式的值恒為一個不變的數,那么小智所取的字母n的值是多少呢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,D為BC中點,BE、CF與射線AE分別相交于點E、F(射線AE不經過點D).
(1)如圖①,當BE∥CF時,連接ED并延長交CF于點H. 求證:四邊形BECH是平行四邊形;
(2)如圖②,當BE⊥AE于點E,CF⊥AE于點F時,分別取AB、AC的中點M、N,連接ME、MD、NF、ND. 求證:∠EMD=∠FND.


圖① 圖②
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,對角線AC、BD相交于點O,過點C作CE∥BD,過點D作DE∥AC,CE與DE相交于點E.
(1)求證:四邊形CODE是矩形.
(2)若AB=5,AC=6,求四邊形CODE的周長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,小東用長為3.2m的竹竿做測量工具測量學校旗桿的高度,移動竹竿,使竹竿、旗桿頂端的影子恰好落在地面的同一點.此時,竹竿與這一點相距8m,與旗桿相距22m,則旗桿的高為( ) 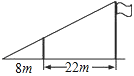
A.12m
B.10m
C.8m
D.7m
查看答案和解析>>
科目:初中數學 來源: 題型:
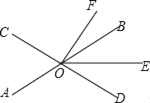
【題目】如圖,直線AB、CD相交于點O,OE平分∠BOD.
(1)若∠AOC=68°,∠DOF=90°,求∠EOF的度數.
(2)若OF平分∠COE,∠BOF=30°,求∠AOC的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com