
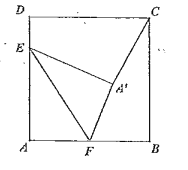
【題目】如圖,在邊長為![]() 的正方形
的正方形![]() 中,點(diǎn)
中,點(diǎn)![]() 為靠近點(diǎn)
為靠近點(diǎn)![]() 的四等分點(diǎn),點(diǎn)
的四等分點(diǎn),點(diǎn)![]() 為
為![]() 中點(diǎn),將
中點(diǎn),將![]() 沿
沿![]() 翻折得到
翻折得到![]() 連接
連接![]() 則點(diǎn)
則點(diǎn)![]() 到
到![]() 所在直線距離為________________.
所在直線距離為________________.
【答案】![]()
【解析】
延長![]() 交BC于點(diǎn)M,連接FM,延長
交BC于點(diǎn)M,連接FM,延長![]() 交DA的延長線于點(diǎn)P,作DN⊥CP,先證明
交DA的延長線于點(diǎn)P,作DN⊥CP,先證明![]() ∽
∽![]() ,利用相似的性質(zhì)求出
,利用相似的性質(zhì)求出![]() ,然后證明
,然后證明![]() ∽
∽![]() ,利用相似的性質(zhì)求出EP,從而得到DP的長,再利用勾股定理求出CP的長,最后利用等面積法計(jì)算DN即可.
,利用相似的性質(zhì)求出EP,從而得到DP的長,再利用勾股定理求出CP的長,最后利用等面積法計(jì)算DN即可.
如圖,延長![]() 交BC于點(diǎn)M,連接FM,延長
交BC于點(diǎn)M,連接FM,延長![]() 交DA的延長線于點(diǎn)P,作DN⊥CP,
交DA的延長線于點(diǎn)P,作DN⊥CP,

由題可得,![]() ,
,![]() ,
,
∴![]() ,
,
∵F為AB中點(diǎn),
∴![]() ,
,
又∵FM=FM,
∴![]() ≌
≌![]() (HL),
(HL),
∴![]() ,
,![]() ,
,
由折疊可知,![]() ,
,
∴![]() ,
,
又∵![]()
∴![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,
,
∵AD=4,E為四等分點(diǎn),
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,即
,即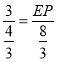 ,
,
∴EP=6,
∴DP=EP+DE=7,
在![]() 中,
中,![]() ,
,
∵![]() ,
,
∴![]() .
.
故答案為:![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖在⊙O中,BC=2,AB=AC,點(diǎn)D為AC上的動點(diǎn),且cosB=![]() .
.
(1)求AB的長度;
(2)求ADAE的值;
(3)過A點(diǎn)作AH⊥BD,求證:BH=CD+DH.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為提高飲水質(zhì)量,越來越多的居民選擇家用凈水器,光明商場計(jì)劃從生產(chǎn)廠家購進(jìn)甲、乙兩種型號的家用凈水器,甲型號凈水器進(jìn)價(jià)為160元/臺,乙型號凈水器進(jìn)價(jià)為280元/臺,經(jīng)過協(xié)商溝通,生產(chǎn)廠家拿出了兩種優(yōu)惠方案:第一種優(yōu)惠方案:甲、乙兩種型號凈水器均按進(jìn)價(jià)的8折收費(fèi);第二種優(yōu)惠方案:甲型號凈水器按原價(jià)收費(fèi),乙型號凈水器的進(jìn)貨量超過10臺后超過的部分按進(jìn)價(jià)的6折收費(fèi).
光明商場只能選擇一種優(yōu)惠方案,已知光明商場計(jì)劃購進(jìn)甲型號凈水器數(shù)量是乙型號凈水器數(shù)量的1.5倍,設(shè)光明商場購進(jìn)乙型號凈水器![]() 臺,選擇第一種優(yōu)惠方案所需費(fèi)用為片
臺,選擇第一種優(yōu)惠方案所需費(fèi)用為片![]() 元,選擇第二種優(yōu)惠方案所需費(fèi)用為
元,選擇第二種優(yōu)惠方案所需費(fèi)用為![]() 元.
元.
(1)分別求出![]() 、
、![]() 與
與![]() 的關(guān)系式:
的關(guān)系式:
(2)光明商場計(jì)劃購進(jìn)乙型號凈水器40臺,請你為光明商場選擇合適的優(yōu)惠方案,并說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在⊙O中,AB為直徑,C為⊙O上一點(diǎn).
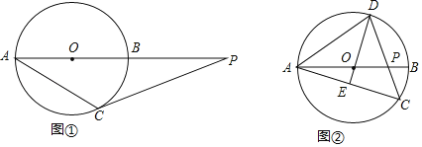
(Ⅰ)如圖①,過點(diǎn)C作⊙O的切線,與AB的延長線相交于點(diǎn)P,若∠CAB=32°,求∠P的大小;
(Ⅱ)如圖②,D為優(yōu)弧ADC上一點(diǎn),且DO的延長線經(jīng)過AC的中點(diǎn)E,連接DC與AB相交于點(diǎn)P,若∠CAB=16°,求∠DPA的大小.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】我校小偉同學(xué)酷愛健身,一天去爬山鍛煉,在出發(fā)點(diǎn)C處測得山頂部A的仰角為30度,在爬山過程中,每一段平路(CD、EF、GH)與水平線平行,每一段上坡路(DE、FG、HA)與水平線的夾角都是45度,在山的另一邊有一點(diǎn)B(B、C、D同一水平線上),斜坡AB的坡度為2:1,且AB長為900![]() ,其中小偉走平路的速度為65.7米/分,走上坡路的速度為42.3米/分.則小偉從C出發(fā)到坡頂A的時(shí)間為( )(圖中所有點(diǎn)在同一平面內(nèi)
,其中小偉走平路的速度為65.7米/分,走上坡路的速度為42.3米/分.則小偉從C出發(fā)到坡頂A的時(shí)間為( )(圖中所有點(diǎn)在同一平面內(nèi)![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
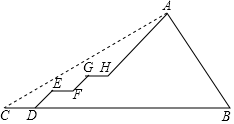
A.60分鐘B.70分鐘C.80分鐘D.90分鐘
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
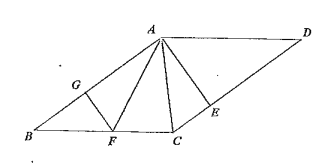
【題目】在平行四邊形![]() 中,
中,![]() 為對角線,
為對角線,![]() ,點(diǎn)
,點(diǎn)![]() 分別為
分別為![]() 邊上的點(diǎn),連接
邊上的點(diǎn),連接![]() 平分
平分![]() .
.
(1)如圖,若![]() 且
且![]() ,求平行四邊形
,求平行四邊形![]() 的面積.
的面積.
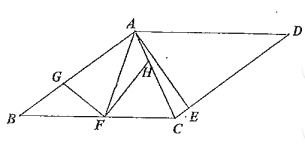
(2)如圖,若![]() 過
過![]() 作
作![]() 交
交![]() 于
于![]() 求證:
求證:![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,矩形EFGH的頂點(diǎn)E,G分別在菱形ABCD的邊AD,BC上,頂點(diǎn)F,H在菱形ABCD的對角線BD上.

(1)求證:BG=DE;
(2)若E為AD中點(diǎn),FH=2,求菱形ABCD的周長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(1)如圖1,已知:在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() 分別在
分別在![]() 上,連接
上,連接![]() ,點(diǎn)
,點(diǎn)![]() 為線段
為線段![]() 的中點(diǎn),連接
的中點(diǎn),連接![]() ,則線段
,則線段![]() 與
與![]() 之間的數(shù)量關(guān)系是 ,位置關(guān)系是
之間的數(shù)量關(guān)系是 ,位置關(guān)系是

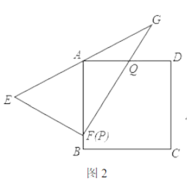
(2)如圖2所示,已知:正方形![]() 將
將![]() 斜邊
斜邊![]() 的中點(diǎn)與點(diǎn)
的中點(diǎn)與點(diǎn)![]() 重合,直角頂點(diǎn)
重合,直角頂點(diǎn)![]() 落在正方形的
落在正方形的![]() 邊上,
邊上,![]() 的兩直角邊分別交
的兩直角邊分別交![]() 邊于
邊于![]() 兩點(diǎn)(點(diǎn)
兩點(diǎn)(點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 重合),求證:
重合),求證:![]() ;
;
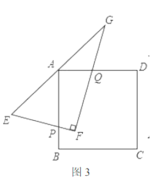
(3)如圖3,若將![]() 繞著點(diǎn)
繞著點(diǎn)![]() 逆時(shí)針旋轉(zhuǎn)
逆時(shí)針旋轉(zhuǎn)![]() ,兩直角邊分別交
,兩直角邊分別交![]() 邊于
邊于![]() 兩點(diǎn),如圖3所示:判斷四條線段
兩點(diǎn),如圖3所示:判斷四條線段![]() 之間是否存在什么確定的相等關(guān)系?若存在,證明你的結(jié)論.若不存在,請說明理由.
之間是否存在什么確定的相等關(guān)系?若存在,證明你的結(jié)論.若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】行駛中的汽車,在剎車后由于慣性的原因,還要繼續(xù)向前滑行一段距離才能停住,這段距離稱為“剎車距離”.為了測定某種型號汽車的剎車性能,對這種汽車的剎車距離進(jìn)行測試,測得的數(shù)據(jù)如下表:
剎車時(shí)車速(千米/時(shí)) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
剎車距離(米) | 0 | 0.1 | 0.3 | 0.6 | 1 | 1.6 | 2.1 |
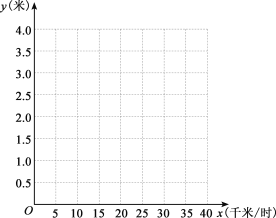
(1)在如圖所示的直角坐標(biāo)系中,以剎車時(shí)車速為橫坐標(biāo),以剎車距離為縱坐標(biāo),描出這些數(shù)據(jù)所表示的點(diǎn),并用平滑的曲線連結(jié)這些點(diǎn),得到某函數(shù)的大致圖象;
(2)測量必然存在誤差,通過觀察圖象估計(jì)函數(shù)的類型,求出一個(gè)大致滿足這些數(shù)據(jù)的函數(shù)表達(dá)式;
(3)一輛該型號汽車在高速公路上發(fā)生交通事故,現(xiàn)場測得剎車距離約為40米,已知這條高速公路限速100千米/時(shí),請根據(jù)你確定的函數(shù)表達(dá)式,通過計(jì)算判斷在事故發(fā)生時(shí),汽車是否超速行駛.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com