
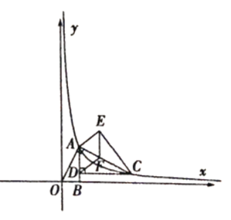
【題目】已知:如圖,![]() 的頂點
的頂點![]() 是反比例函數
是反比例函數![]() 圖象上一點,過點
圖象上一點,過點![]() 作
作![]() 交反比例函數的圖象于點
交反比例函數的圖象于點![]() ,過點
,過點![]() 作
作![]() 于點
于點![]()
(1)求點![]() 的坐標;
的坐標;
(2)將![]() 沿
沿![]() 翻折得到
翻折得到![]() ,過點
,過點![]() 作
作![]() 軸交
軸交![]() 于點
于點![]() ,連接
,連接![]() ,判斷四邊形
,判斷四邊形![]() 的形狀并說明理由.
的形狀并說明理由.
【答案】(1)![]() ;(2)四邊形
;(2)四邊形![]() 是菱形,理由見解析
是菱形,理由見解析
【解析】
(1)先根據A點坐標求出反比例函數解析式,然后證明![]() ,利用對應邊成比例得到
,利用對應邊成比例得到![]() ,設
,設![]() ,則點
,則點![]() 在反比例函數
在反比例函數![]() 的圖象上,解出t的值,即可得C點坐標;
的圖象上,解出t的值,即可得C點坐標;
(2)連接![]() ,交
,交![]() 于點
于點![]() ,由折疊得到性質可得
,由折疊得到性質可得![]() ,然后證明
,然后證明![]() ,得到AD=EF即可得出四邊形ADFE為平行四邊形,加上對角線互相垂直即可判定為菱形.
,得到AD=EF即可得出四邊形ADFE為平行四邊形,加上對角線互相垂直即可判定為菱形.
解:(1)∵點![]() 在反比例函數
在反比例函數![]() 圖象上,
圖象上,
∴![]() ,即
,即![]()
∵![]() ,
,
∴![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]()
設![]() ,則點
,則點![]() 在反比例函數
在反比例函數![]() 的圖象上,
的圖象上,
∴![]() ,解得
,解得![]() (舍去),
(舍去),![]() ,
,
∴C點橫坐標=1+2×![]() =4,縱坐標=
=4,縱坐標=![]()
即點![]()
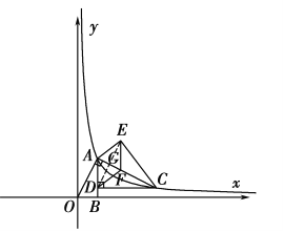
(2)四邊形![]() 是菱形.理由如下:
是菱形.理由如下:
∵將![]() 沿
沿![]() 翻折得到
翻折得到![]() ,
,
∴![]() ,點
,點![]() 關于
關于![]() 對稱.
對稱.
如圖,連接![]() ,交
,交![]() 于點
于點![]() ,則DE⊥AF,
,則DE⊥AF,![]() .
.
易證![]() ,
,
∴![]() .
.
∵![]() ,
,
∴四邊形![]() 為平行四邊形,
為平行四邊形,
又∵DE⊥AF
∴四邊形![]() 是菱形.
是菱形.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】甲、乙、丙、丁四位同學進行乒乓球單打比賽,要從中選出兩位同學打第一場比賽.
(1) 若確定甲打第一場,再從其余三位同學中隨機選取一位,恰好選中乙同學的概率是 .
(2) 若隨機抽取兩位同學,請用畫樹狀圖法或列表法,求恰好選中甲、乙兩位同學的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為實施“農村留守兒童關愛計劃”,某校結全校各班留守兒童的人數情況進行了統計,發現各班留守兒童人數只有1名、2名、3名、4名、5名、6名共六種情況,并制成如下兩幅不完整的統計圖:
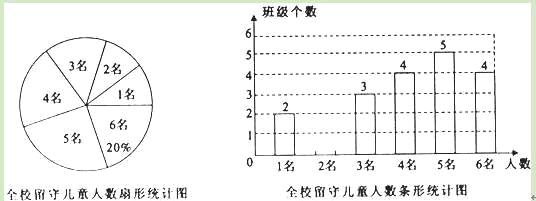
(1)求該校平均每班有多少名留守兒童?并將該條形統計圖補充完整;
(2)某愛心人士決定從只有2名留守兒童的這些班級中,任選兩名進行生活資助,請用列表法或畫樹狀圖的方法,求出所選兩名留守兒童來自同一個班級的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合與實踐:
問題情境:已知![]() 是正方形
是正方形![]() 的對角線,將直角三角尺放在正方形
的對角線,將直角三角尺放在正方形![]() 上.
上.
(1)如圖1,使三角尺的直角頂點與點![]() 重合,三角尺的一條直角邊交直線
重合,三角尺的一條直角邊交直線![]() 于點
于點![]() ,另一條直角邊交直線
,另一條直角邊交直線![]() 于點
于點![]() .求證:
.求證:![]() .
.
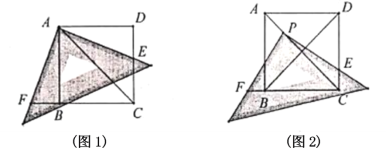
操作發現:
(2)如圖2,將三角尺的直角項點![]() 放在
放在![]() 上,三角尺的一條直角邊交直線
上,三角尺的一條直角邊交直線![]() 于點
于點![]() ,另一條直角邊交直線
,另一條直角邊交直線![]() 于點
于點![]() .判斷
.判斷![]() 和
和![]() 的數量關系,并說明理由.
的數量關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程x2-(m+2)x+(2m-1)=0。
(1)求證:方程恒有兩個不相等的實數根;
(2)若此方程的一個根是1,請求出方程的另一個根,并求以此兩根為邊長的直角三角形的周長。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某水果公司以22元/千克的成本價購進1000kg蘋果,公司想知道蘋果的損壞率,隨機抽取若干進行統計,部分結果如下表:
草果總質量n(kg) | 100 | 200 | 300 | 400 | 500 | 1000 |
損壞蘋果質量m(kg) | 10.60 | 19.42 | 30.63 | 39.24 | 49.54 | 101.10 |
蘋果損壞的頻率 (結果保留小數點后三位) | 0.106 | 0.097 | 0.102 | 0.098 | 0.099 | 0.101 |
根據此表估計這批蘋果損壞的概率(精確到0.1),從而計算該公司希望這批蘋果能獲得利潤23000元,則銷售時(去掉損壞的蘋果)售價應至少定為_____元/千克.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,以AB為直徑的⊙O交AC于點D,過點D作DE⊥BC于點E,且∠BDE=∠A.
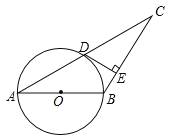
(1)判斷DE與⊙O的位置關系,并說明理由;
(2)若AC=16,tanA=![]() ,求⊙O的半徑.
,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y1=kx+b的圖象與反比例函數y2=![]() 的圖象交于A(2,3),B(6,n)兩點.
的圖象交于A(2,3),B(6,n)兩點.
(1)分別求出一次函數與反比例函數的解析式;
(2)求△OAB的面積.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com