
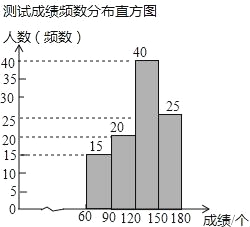
【題目】七中育才學校排球活動月即將開始,其中有一項為墊球比賽,體育組為了了解七年級學生的訓練情況,隨機抽取了七年級部分學生進行1分鐘墊球測試,并將這些學生的測試成績(即1分鐘的個數,且這些測試成績都在60~180范圍內)分段后給出相應等級,具體為:測試成績在60~90范圍內的記為D級,90~120范圍內的記為C級,120~150范圍內的記為B級,150~180范圍內的記為A級.現將數據整理繪制成如下兩幅不完整的統計圖,其中在扇形統計圖中A級對應的圓心角為90°,請根據圖中的信息解答下列問題:
(1)在扇形統計圖中,A級所占百分比為 ;
(2)在這次測試中,一共抽取了 名學生,并補全頻數分布直方圖;
(3)在(2)中的基礎上,在扇形統計圖中,求D級對應的圓心角的度數;
(4)若A,B,C,D等級的平均成績分別為165、135、105、75個,你能估算出學校七年級同學的平均水平嗎?若能,請計算出來.(保留準確值)

【答案】(1)25%(2)100(3)54°(4)能
【解析】
(1)根據A級所在扇形的圓心角為90°求得其所占的百分比即可;
(2)用A級的人數除以其所占的百分比即可求得總人數;
(3)用D級的人數除以總人數乘以周角的度數即可求得對應的圓心角的度數;
(4)能,用樣本估計整體即可算出.
(1)∵A級所在扇形的圓心角的度數為90°,
∴A級所占百分比為![]() ×100%=25%;
×100%=25%;
故答案為:25%;
(2)∵A級有25人,占25%,
∴抽查的總人數為25÷25%=100人,
∴D級有100﹣20﹣40﹣25=15人,
故答案為:100;
頻數分布圖為:
(3)D類的圓心角為:![]() ×360°=54°;
×360°=54°;
(4)能,七年級同學的平均水平為:![]() =108.75.
=108.75.


科目:初中數學 來源: 題型:
【題目】如圖,PA為⊙O的切線,A為切點,過A作OP的垂線AB,垂足為點C,交⊙O于點B,延長BO與⊙O交于點D,與PA的延長線交于點E. 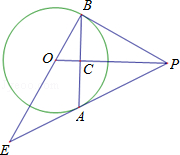
(1)求證:PB為⊙O的切線;
(2)若tan∠ABE= ![]() ,求sin∠E.
,求sin∠E.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一塊長方體木塊的各棱長如圖所示,一只蜘蛛在木塊的一個頂點A處,一只蒼蠅在這個長方體上和蜘蛛相對的頂點B處,蜘蛛急于捉住蒼蠅,沿著長方體的表面向上爬.
(1)如果D是棱的中點,蜘蛛沿“AD→DB”路線爬行,它從A點爬到B點所走的路程為多少?
(2)你認為“AD→DB”是最短路線嗎?如果你認為不是,請計算出最短的路程.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知方程:①3x﹣1=2x+1,②![]() ,③
,③![]() ,④
,④![]() x﹣1=x中,解為x=2的是方程( )
x﹣1=x中,解為x=2的是方程( )
A. ①、②和③ B. ①、③和④ C. ②、③和④ D. ①、②和④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】同學們,足球是世界上第一大運動,你熱愛足球運動嗎?已知在足球比賽中,勝一場得3分,平一場得1分,負一場得0分,一隊共踢了30場比賽,負了9場,共得47分,那么這個隊勝了( )
A. 10場 B. 11場 C. 12場 D. 13場
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若點A、B、C在數軸上對應的數分別為a、b、c滿足|a+5|+|b-1|+|c-2|=0.
(1)在數軸上是否存在點P,使得PA+PB=PC?若存在,求出點P對應的數;若不存在,請說明理由;
(2)若點A,B,C同時開始在數軸上分別以每秒1個單位長度,每秒3個單位長度,每秒5個單位長度沿著數軸負方向運動.經過t(t≥1)秒后,試問AB-BC的值是否會隨著時間t的變化而變化?請說明理由.
![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com