
【題目】已知關于x的方程ax2+bx+c=0(a≠0),下列說法:①若方程有兩個互為相反數的實數根,則b=0;②若方程ax2+bx+c=0沒有實數根,則方程ax2+bx﹣c=0必有兩個不相等的實根;③若二次三項式ax2+bx+c是完全平方式,則b2﹣4ac=0;④若c=0,則方程必有兩個不相等的實數根.其中正確的是( )
A.①②③B.①③④C.①②④D.②③④
【答案】A
【解析】
根據根與系數的關系可判斷①,根據根的判別式與方程解的關系可判斷②③④.
解:①若方程ax2+bx+c=0(a≠0)有兩個互為相反數的實數根,則兩根的和﹣![]() =0,解得b=0,故①正確;
=0,解得b=0,故①正確;
②若方程ax2+bx+c=0沒有實數根,則△=b2﹣4ac<0,即0≤b2<4ac,而方程ax2+bx﹣c=0的△=b2+4ac>0,故方程ax2+bx﹣c=0必有兩個不相等的實根,故②正確;
③若二次三項式ax2+bx+c是完全平方式,得到ax2+bx+c=0有兩個相等的實根,所以△=b2﹣4ac=0,故③正確;
④若c=0,方程ax2+bx+c=0(a≠0)的△=b2﹣4ac=b2≥0,所以方程兩個實數根,故④不正確;
故選:A.


科目:初中數學 來源: 題型:
【題目】如圖,已知等腰Rt△ABC,∠ACB=90°,CA=CB,以BC為邊向外作等邊△CBA,連接AD,過點C作∠ACB的角平分線與AD交于點E,連接BE.

(1)若AE=2,求CE的長度;
(2)以AB為邊向下作△AFB,∠AFB=60°,連接FE,求證:FA+FB= ![]() FE.
FE.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形網格上有△ABC和△DEF.
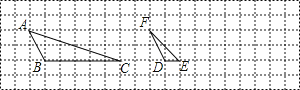
(1)這兩個三角形相似嗎?為什么?
(2)請直接寫出∠A的度數 ;
(3)在上邊的網格內再畫一個三角形,使它與△ABC相似,并求出其相似比.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=x2﹣2x﹣1.
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
| … |
(1)請在表內的空格中填入適當的數;
(2)根據列表,請在所給的平面直角坐標系中畫出y=x2﹣2x﹣1的圖象;
(3)當x在什么范圍內時,y隨x增大而減小;
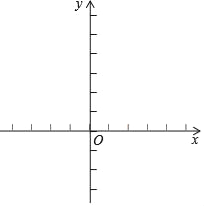
查看答案和解析>>
科目:初中數學 來源: 題型:
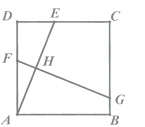
【題目】如圖,在正方形ABCD中,AD=6,點E是邊CD上的動點(點E不與端點C,D重合),AE的垂直平分線FG分別交AD,AE,BC于點F,H,G.當![]() =
=![]() 時,DE的長為( )
時,DE的長為( )
A. 2 B. ![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 某校為了解九年級男同學的體育考試準備情況,隨機抽取部分男同學進行了1000米跑測試.按照成績分為優秀、良好、合格與不合格四個等級.學校繪制了如下不完整的統計圖.
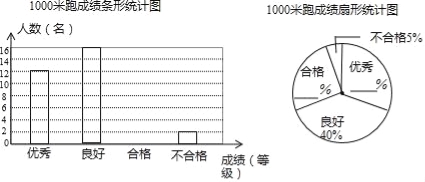
(1)根據給出的信息,補全兩幅統計圖;
(2)該校九年級有600名男生,請估計成績未達到良好有多少名?
(3)某班甲、乙兩位成績優秀的同學被選中參加即將舉行的學校運動會1000米比賽,預賽分為A、B、C三組進行,選手由抽簽確定分組.甲、乙兩人恰好分在同一組的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,可以自由轉動的轉盤被它的兩條直徑分成了四個分別標有數字的扇形區域,其中標有數字“1”的扇形圓心角為120°.轉動轉盤,待轉盤自動停止后,指針指向一個扇形的內部,則該扇形內的數字即為轉出的數字,此時,稱為轉動轉盤一次(若指針指向兩個扇形的交線,則不計轉動的次數,重新轉動轉盤,直到指針指向一個扇形的內部為止)
(1)轉動轉盤一次,求轉出的數字是-2的概率;
(2)轉動轉盤兩次,用樹狀圖或列表法求這兩次分別轉出的數字之積為正數的概率.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com