
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,邊長為
,邊長為![]() 的正方形的一個頂點
的正方形的一個頂點![]() 在邊
在邊![]() 上,與
上,與![]() 另兩邊分
另兩邊分

別交于點![]() 、
、![]() ,
,![]() ,將正方形平移,使點
,將正方形平移,使點![]() 保持在
保持在![]() 上(
上(![]() 不與
不與![]() 重合),設
重合),設![]() ,正方形與
,正方形與![]() 重疊部分的面積為
重疊部分的面積為![]() .
.
![]() 求
求![]() 與
與![]() 的函數關系式并寫出自變量
的函數關系式并寫出自變量![]() 的取值范圍;
的取值范圍;
![]() 為何值時
為何值時![]() 的值最大?
的值最大?
![]() 在哪個范圍取值時
在哪個范圍取值時![]() 的值隨
的值隨![]() 的增大而減小?
的增大而減小?
【答案】(1)![]() ,自變量
,自變量![]() 的取值范圍是
的取值范圍是![]() ;(2)當
;(2)當![]() 時,
時,![]() 有最大值;(3)當
有最大值;(3)當![]() 時,
時,![]() 隨
隨![]() 的增大而減小.
的增大而減小.
【解析】
(1)當點![]() 保持在
保持在![]() 上時,正方形與
上時,正方形與![]() 重疊部分為直角梯形
重疊部分為直角梯形![]() ,根據直角梯形的面積公式,只需用含
,根據直角梯形的面積公式,只需用含![]() 的代數式分別表示出上底
的代數式分別表示出上底![]() 、下底
、下底![]() 及高
及高![]() 的長度即可.由
的長度即可.由![]() 為等腰直角三角形,可得高
為等腰直角三角形,可得高![]() ,則
,則![]() ,下底
,下底![]() ,進而得到
,進而得到![]() ,再根據等腰三角形及平行線的性質可證
,再根據等腰三角形及平行線的性質可證![]() ,得出上底
,得出上底![]() ,根據點
,根據點![]() 保持在
保持在![]() 上,且
上,且![]() 不與
不與![]() 重合,可知
重合,可知![]() ,從而求出自變量
,從而求出自變量![]() 的取值范圍;
的取值范圍;
(2)由(1)知,![]() 是
是![]() 的二次函數,根據二次函數的性質,可知當
的二次函數,根據二次函數的性質,可知當![]() 時,
時,![]() 的值最大;
的值最大;
(3)根據二次函數的增減性,當![]() 時,在對稱軸
時,在對稱軸![]() 的右側,
的右側,![]() 的值隨
的值隨![]() 的增大而減小.
的增大而減小.
解:![]() ∵
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
在![]() 中,∵
中,∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵點![]() 保持在
保持在![]() 上,且
上,且![]() 不與
不與![]() 重合,
重合,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
故![]() ,自變量
,自變量![]() 的取值范圍是
的取值范圍是![]() ;
;
![]() ∵
∵![]() ,
,
∴當![]() 時,
時,![]() 有最大值;
有最大值;
![]() ∵
∵![]() ,
,![]() ,
,![]() ,
,
∴當![]() 時,
時,![]() 隨
隨![]() 的增大而減小.
的增大而減小.


科目:初中數學 來源: 題型:
【題目】△ABC中,∠BAC=90°,AB=AC,點D為直線BC上一動點(點D不與B,C重合),以AD為邊在AD右側作正方形ADEF,連接CF.
(1)觀察猜想
如圖1,當點D在線段BC上時,
①BC與CF的位置關系為: .
②BC,CD,CF之間的數量關系為: ;(將結論直接寫在橫線上)
(2)數學思考
如圖2,當點D在線段CB的延長線上時,結論①,②是否仍然成立?若成立,請給予證明;若不成立,請你寫出正確結論再給予證明.
(3)拓展延伸
如圖3,當點D在線段BC的延長線上時,延長BA交CF于點G,連接GE.若已知AB=2![]() ,CD=
,CD=![]() BC,請求出GE的長.
BC,請求出GE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,E是平行四邊形ABCD的邊AD上的一動點(點E不與A、D重合),連結CE并延長交BA的延長線于點F。
(1) △CDE與△FAE是否總相似?為什么?
(2)當E點為AD的中點時,求證:CE=EF;
(3)當E點移至使EC⊥BC時,設AB=4cm,EF=6cm,∠D=60°時,求CB的長。(結果不取近似值)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場投入13 800元資金購進甲、乙兩種礦泉水共500箱,礦泉水的成本價和銷售價如表所示:
類別/單價 | 成本價 | 銷售價(元/箱) |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)該商場購進甲、乙兩種礦泉水各多少箱?
(2)全部售完500箱礦泉水,該商場共獲得利潤多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了預防“流感”,某學校對教室采用藥熏消毒法進行消毒,已知藥物燃燒時,室內每立方米空氣中的含藥量![]() 與時間
與時間![]() 成正比例,藥物燃燒完后,
成正比例,藥物燃燒完后,![]() 與
與![]() 成反比例(如圖所示).現測得藥物
成反比例(如圖所示).現測得藥物![]() 燃畢,此時室內空氣中每立方米的含藥量為
燃畢,此時室內空氣中每立方米的含藥量為![]() .研究表明,當空氣中每立方米的含藥量不低于
.研究表明,當空氣中每立方米的含藥量不低于![]() 才有效,那么此次消毒的有效時間是( )
才有效,那么此次消毒的有效時間是( )

A. ![]() 分鐘 B.
分鐘 B. ![]() 分鐘 C.
分鐘 C. ![]() 分鐘 D.
分鐘 D. ![]() 分鐘
分鐘
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,長方形ABCD中AD∥BC,邊AB=4,BC=8.將此長方形沿EF折疊,使點D與點B重合,點C落在點G處.
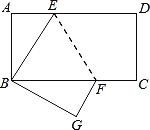
(1)試判斷△BEF的形狀,并說明理由;
(2)若AE=3,求△BEF的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com