Question

如圖，在等腰三角形ABC中，AB=AC=10cm，∠ABC=30⁰，以BC所在直線為x軸，以BC邊上的高所在的直線為y軸建立平面直角三角形系。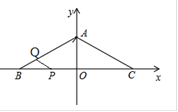

（1）求直線AC的解析式；
（2）有一動點P以1cm/s的速度從點B開始沿x軸向其正方向運動，設點P的運動為t秒（單位：s）。
①當t為何值時，ΔABP是直角三角形；
②現有另一點Q與點P同時從點B開始，以1cm/s的速度從點B開始沿折線BAC運動，當點Q到達點C時，P、Q兩點同時停止運動。試寫出ΔBPQ的面積S關于t的函數解析式，并寫出自變量的取值范圍。

Answer 1

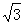（1）y=-x+5  （2）t=5；t=
（3）當0<t<10時，S=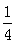t²；10<t≤20時，S=-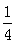t²+5t

解析試題分析：（1）AC=10，∠ABC=30⁰因為是等腰三角形ABC，所以OA="5" ，從而可得到OC=5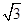.那么A(0，5),C(5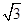,0),設直線AC的解析式為y=ax+b，代入A,C兩點，得y=-x+5
（2）ΔABP是直角三角形也即p點運動到0點，即運動的距離為線段BO，BO=OC。所以運動的時間為5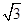s
當∠BAP=90⁰時，此時的P點在X軸的正半軸。此時的p點可設為（x,0）,由題可得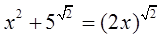,即X=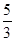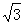,加上前面的5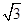，得到t=
（3）0<t<10，即Q在BA點運動時，S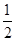=txtx=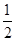
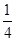
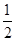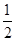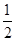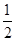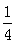10<t≤20,Q在AC上運動，設此時Q的坐標為（m,m+5）,再由5-(m+5)=(t-10)x得出Q點的縱坐標為10-t,圍成的三角形面積=tx(10-t )x=-t²+5t
考點：函數的解析式的求法，三角形的面積。
點評：此題較難。有很強的綜合性。要求考生基礎扎實，對問題有較強的分析能力。