
【題目】如圖,AB是⊙O的一條弦,E是AB的中點,過點E作EC⊥OA于點C,過點B作⊙O的切線交CE的延長線于點D. 
(1)求證:DB=DE;
(2)若AB=12,BD=5,求⊙O的半徑.
【答案】
(1)證明:∵AO=OB,
∴∠OAB=∠OBA,
∵BD是切線,
∴OB⊥BD,
∴∠OBD=90°,
∴∠OBE+∠EBD=90°,
∵EC⊥OA,
∴∠CAE+∠CEA=90°,
∵∠CEA=∠DEB,
∴∠EBD=∠BED,
∴DB=DE
(2)作DF⊥AB于F,連接OE.
∵DB=DE,AE=EB=6,
∴EF= ![]() BE=3,OE⊥AB,
BE=3,OE⊥AB,
在Rt△EDF中,DE=BD=5,EF=3,
∴DF= ![]() =4,
=4,
∵∠AOE+∠A=90°,∠DEF+∠A=90°,
∴∠AOE=∠DEF,
∴sin∠DEF=sin∠AOE= ![]() =
= ![]() ,
,
∵AE=6,
∴AO= ![]() .
.
∴⊙O的半徑為 ![]() .
.

【解析】(1)欲證明DB=DE,只要證明∠DEB=∠DBE;(2)作DF⊥AB于F,連接OE.只要證明∠AOE=∠DEF,可得sin∠DEF=sin∠AOE= ![]() =
= ![]() ,由此求出AE即可解決問題.
,由此求出AE即可解決問題.
【考點精析】認真審題,首先需要了解勾股定理的概念(直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2),還要掌握垂徑定理(垂徑定理:平分弦(不是直徑)的直徑垂直于弦,并且平分弦所對的兩條弧)的相關知識才是答題的關鍵.


科目:初中數學 來源: 題型:
【題目】如圖,大樓AB右側有一障礙物,在障礙物的旁邊有一幢小樓DE,在小樓的頂端D處測得障礙物邊緣點C的俯角為30°,測得大樓頂端A的仰角為45°(點B,C,E在同一水平直線上),已知AB=80m,DE=10m,求障礙物B,C兩點間的距離(結果精確到0.1m)(參考數據: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)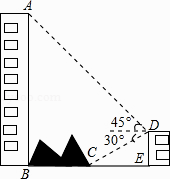
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=﹣x+b與反比例函數y= ![]() (x>0)的圖象交于點A(m,3)和B(3,1).
(x>0)的圖象交于點A(m,3)和B(3,1). 
(1)填空:一次函數的解析式為 , 反比例函數的解析式為;
(2)點P是線段AB上一點,過點P作PD⊥x軸于點D,連接OP,若△POD的面積為S,求S的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲乙兩個施工隊在六安(六盤水﹣安順)城際高鐵施工中,每天甲隊比乙隊多鋪設100米鋼軌,甲隊鋪設5天的距離剛好等于乙隊鋪設6天的距離.若設甲隊每天鋪設x米,乙隊每天鋪設y米.
(1)依題意列出二元一次方程組;
(2)求出甲乙兩施工隊每天各鋪設多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中的點P和圖形M,給出如下的定義:若在圖形M上存在一點Q,使得P、Q兩點間的距離小于或等于1,則稱P為圖形M的關聯點.
(1)當⊙O的半徑為2時,
①在點P1( ![]() ,0),P2(
,0),P2( ![]() ,
, ![]() ),P3(
),P3( ![]() ,0)中,⊙O的關聯點是 .
,0)中,⊙O的關聯點是 .
②點P在直線y=﹣x上,若P為⊙O的關聯點,求點P的橫坐標的取值范圍.
(2)⊙C的圓心在x軸上,半徑為2,直線y=﹣x+1與x軸、y軸交于點A、B.若線段AB上的所有點都是⊙C的關聯點,直接寫出圓心C的橫坐標的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=2x與反比例函數y= ![]() (k≠0,x>0)的圖象交于點A(1,a),B是反比例函數圖象上一點,直線OB與x軸的夾角為α,tanα=
(k≠0,x>0)的圖象交于點A(1,a),B是反比例函數圖象上一點,直線OB與x軸的夾角為α,tanα= ![]() .
. 
(1)求k的值.
(2)求點B的坐標.
(3)設點P(m,0),使△PAB的面積為2,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“420”雅安地震后,某商家為支援災區人民,計劃捐贈帳篷16800頂,該商家備有2輛大貨車、8輛小貨車運送帳篷.計劃大貨車比小貨車每輛每次多運帳篷200頂,大、小貨車每天均運送一次,兩天恰好運完.
(1)求大、小貨車原計劃每輛每次各運送帳篷多少頂?
(2)因地震導致路基受損,實際運送過程中,每輛大貨車每次比原計劃少運200m頂,每輛小貨車每次比原計劃少運300頂,為了盡快將帳篷運送到災區,大貨車每天比原計劃多跑 ![]() m次,小貨車每天比原計劃多跑m次,一天恰好運送了帳篷14400頂,求m的值.
m次,小貨車每天比原計劃多跑m次,一天恰好運送了帳篷14400頂,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,⊙C過原點,且與兩坐標軸分別交于點A、點B,點A的坐標為(0,3),M是第三象限內 ![]() 上一點,∠BMO=120°,則⊙C的半徑長為( )
上一點,∠BMO=120°,則⊙C的半徑長為( ) 
A.6
B.5
C.3
D.3 ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com