【題目】如圖，五邊形ABCDE的各內角相等．
（1）求每個內角的度數；
（2）連接AC，AD，∠1＝∠2，∠3＝∠4，求∠CAD的度數．
科目：初中數學 來源： 題型：
【題目】如圖，菱形
中，
，
，點
在
上，
，過點作
，交
于
，點
從點
出發以
個單位
的速度沿著線段向終點
運動，同時點
從點出發也以個單位的速度沿著線段
向終點運動，設運動時間為
．
填空：當
時，
________；
當
平分
時，直線
將菱形的周長分成兩部分，求這兩部分的比；
以為圓心，長為半徑的
是否能與直線
相切？如果能，求此時
的值；如果不能，說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小明和幾位同學做手的影子游戲時，發現對于同一物體，影子的大小與光源到物體的距離有關．因此，他們認為：可以借助物體的影子長度計算光源到物體的位置．于是，他們做了以下嘗試．
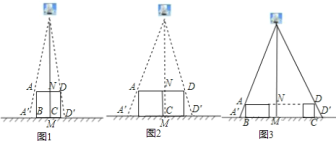
如圖
，垂直于地面放置的正方形框架
，邊長
為
，在其正上方有一燈泡，在燈泡的照射下，正方形框架的橫向影子
，
的長度和為
．那么燈泡離地面的高度為________．
不改變圖中燈泡的高度，將兩個邊長為的正方形框架按圖
擺放，請計算此時橫向影子，的長度和為多少？
有
個邊長為
的正方形按圖
擺放，測得橫向影子，的長度和為
，求燈泡離地面的距離．（寫出解題過程，結果用含，，的代數式表示）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】圖形的變換趣味無窮，如圖①，在平面直角坐標系中，線段l位于第二象限，A(a，b)是線段l上一點，對于線段我們也可以做一些變換：
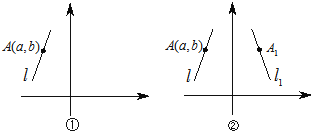
（1）如圖②，將線段l以y軸為對稱軸作軸對稱變換得到線段l1，若點A(
，3)，則點A(，3)關于y軸為對稱軸的點A1的坐標是______.
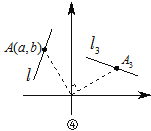
（2）如圖④，將線段l繞坐標原點O順時針方向旋轉90°得到線段l2，則點A(a，b)對應的點A3的坐標是什么？并說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，拋物線y=nx2﹣3nx﹣4n（n＜0）與x軸交于B、C兩點（點B在點C的左側），且拋物線與y軸交于點A．
（1）點B的坐標為 ，點C的坐標為 ；
（2）若∠BAC=90°，求拋物線的解析式．
（3）點M是（2）中拋物線上的動點，點N是其對稱軸上的動點，是否存在這樣的點M、N，使得以A、C、M、N為頂點的四邊形是平行四邊形？若存在，請直接寫出點M的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（1）感知：如圖1，AD平分∠BAC，∠B+∠C＝180°，∠B＝90°，易知DB，DC數量關系為： ．
（2）探究：如圖2，AD平分∠BAC，∠ABD+∠ACD＝180°，∠ABD＜90°，（1）中的結論是否成立？請作出判斷并給予證明．
（3）應用：如圖3，在四邊形ABCD中，DB＝DC，∠ABD+∠ACD＝180°，∠ABD＜90°，DE⊥AB于點E，試判斷AB，AC，BE的數量關系，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1,△ABC和△DEF是兩塊可完全重合的三角板,
,
.在如圖1所示的狀態下,△DEF固定不動,將△ABC沿直線a向左平移.
(1)當△ABC移到圖2位置時,連解AF、DC,求證:AF=DC；
(2)若EF=8,在上述平移過程中,試猜想點C距點E多遠時,線段AD被直線a垂直平分。并證明你的猜想是正確的。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在如圖的正方形網格中，每一個小正方形的邊長為1．格點三角形ABC（頂點是網格線交點的三角形）的頂點A、C的坐標分別是（﹣4，6），（﹣1，4）．
（1）請在圖中的網格平面內建立平面直角坐標系；
（2）請畫出△ABC關于x軸對稱的△A1B1C1；
（3）△ABC 直角三角形（填“是”或“不是”）；
（4）請在y軸上畫一點P，使△PB1C的周長最小，并寫出點P的坐標．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
