
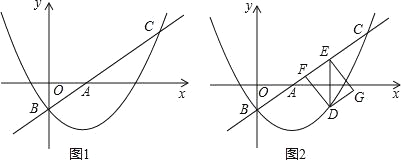
【題目】如圖1,直線l:y=![]() x+m與x軸、y軸分別交于點A和點B(0,﹣1),拋物線y=
x+m與x軸、y軸分別交于點A和點B(0,﹣1),拋物線y=![]() x2+bx+c經過點B,與直線l的另一個交點為C(4,n).
x2+bx+c經過點B,與直線l的另一個交點為C(4,n).
(1)求n的值和拋物線的解析式;
(2)點D在拋物線上,DE∥y軸交直線l于點E,點F在直線l上,且四邊形DFEG為矩形(如圖2),設點D的橫坐標為t(0<t<4),矩形DFEG的周長為p,求p與t的函數關系式以及p的最大值;
(3)將△AOB繞平面內某點M旋轉90°或180°,得到△A1O1B1,點A、O、B的對應點分別是點A1、O1、B1.若△A1O1B1的兩個頂點恰好落在拋物線上,那么我們就稱這樣的點為“落點”,請直接寫出“落點”的個數和旋轉180°時點A1的橫坐標.
【答案】(1)n=2;y=![]() x2﹣
x2﹣![]() x﹣1;(2)p=
x﹣1;(2)p=![]() ;當t=2時,p有最大值
;當t=2時,p有最大值![]() ;(3)
;(3)![]() 或
或![]() ;
;
【解析】
(1)把點B的坐標代入直線解析式求出m的值,再把點C的坐標代入直線求解即可得到n的值,然后利用待定系數法求二次函數解析式解答;
(2)令y=0求出點A的坐標,從而得到OA、OB的長度,利用勾股定理列式求出AB的長,然后根據兩直線平行,內錯角相等可得∠ABO=∠DEF,再解直角三角形用DE表示出EF、DF,根據矩形的周長公式表示出p,利用直線和拋物線的解析式表示DE的長,整理即可得到P與t的關系式,再利用二次函數的最值問題解答;
(3)根據逆時針旋轉角為90°可得A1O1∥y軸時,B1O1∥x軸,旋轉角是180°判斷出A1O1∥x軸時,B1A1∥AB,根據圖3、圖4兩種情形即可解決.
解:
(1)∵直線l:y=![]() x+m經過點B(0,﹣1),
x+m經過點B(0,﹣1),
∴m=﹣1,
∴直線l的解析式為y=![]() x﹣1,
x﹣1,
∵直線l:y=![]() x﹣1經過點C(4,n),
x﹣1經過點C(4,n),
∴n=![]() ×4﹣1=2,
×4﹣1=2,
∵拋物線y=![]() x2+bx+c經過點C(4,2)和點B(0,﹣1),
x2+bx+c經過點C(4,2)和點B(0,﹣1),
∴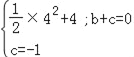 ,
,
解得![]() ,
,
∴拋物線的解析式為y=![]() x2﹣
x2﹣![]() x﹣1;
x﹣1;
(2)令y=0,則![]() x﹣1=0,
x﹣1=0,
解得x=![]() ,
,
∴點A的坐標為(![]() ,0),
,0),
∴OA=![]() ,
,
在Rt△OAB中,OB=1,
∴AB=![]() =
=![]() =
=![]() ,
,
∵DE∥y軸,
∴∠ABO=∠DEF,
在矩形DFEG中,EF=DEcos∠DEF=DE![]() =
=![]() DE,
DE,
DF=DEsin∠DEF=DE![]() =
=![]() DE,
DE,
∴p=2(DF+EF)=2(![]() +
+![]() )DE=
)DE=![]() DE,
DE,
∵點D的橫坐標為t(0<t<4),
∴D(t,![]() t2﹣
t2﹣![]() t﹣1),E(t,
t﹣1),E(t,![]() t﹣1),
t﹣1),
∴DE=(![]() t﹣1)﹣(
t﹣1)﹣(![]() t2﹣
t2﹣![]() t﹣1)=﹣
t﹣1)=﹣![]() t2+2t,
t2+2t,
∴p=![]() ×(﹣
×(﹣![]() t2+2t)=﹣
t2+2t)=﹣![]() t2+
t2+![]() t,
t,
∵p=﹣![]() (t﹣2)2+
(t﹣2)2+![]() ,且﹣
,且﹣![]() <0,
<0,
∴當t=2時,p有最大值![]() .
.
(3)“落點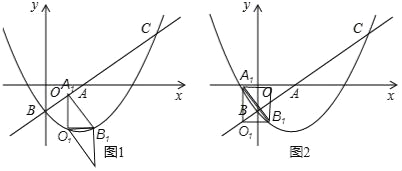
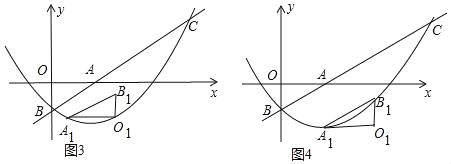
如圖3中,設A1的橫坐標為m,則O1的橫坐標為m+![]() ,
,
∴![]() m2﹣
m2﹣![]() m﹣1=
m﹣1=![]() (m+
(m+![]() )2﹣
)2﹣![]() (m+
(m+![]() )﹣1,
)﹣1,
解得m=![]() ,
,
如圖4中,設A1的橫坐標為m,則B1的橫坐標為m+![]() ,B1的縱坐標比例A1的縱坐標大1,
,B1的縱坐標比例A1的縱坐標大1,
∴![]() m2﹣
m2﹣![]() m﹣1+1=
m﹣1+1=![]() (m+
(m+![]() )2﹣
)2﹣![]() (m+
(m+![]() )﹣1,
)﹣1,
解得m=![]() ,
,
∴旋轉180°時點A1的橫坐標為![]() 或
或![]()


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,一艘漁船正以60海里/小時的速度向正東方向航行,在A處測得島礁P在東北方向上,繼續航行1.5小時后到達B處此時測得島礁P在北偏東30°方向,同時測得島礁P正東方向上的避風港M在北偏東60°方向。為了在臺風到來之前用最短時間到達M處,漁船立刻加速以75海里/小時的速度繼續航行多少小時即可到達? (結果保留根號)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,△ABC的三個頂點坐標都在格點上,且△A1B1C1與△ABC關于原點O成中心對稱,C點坐標為(-2,1)。
(1)請直接寫出A1的坐標 ;并畫出△A1B1C1.
(2)P(a,b)是△ABC的AC邊上一點,將△ABC平移后點P的對稱點P'(a+2,b﹣6),請畫出平移后的△A2B2C2.
(3)若△A1B1C1和△A2B2C2關于某一點成中心對稱,則對稱中心的坐標為 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市對今年“元旦”期間銷售A、B、C三種品牌的綠色雞蛋情況進行了統計,并繪制如圖所示的扇形統計圖和條形統計圖.根據圖中信息解答下列問題:
(1)該超市“元旦”期間共銷售 個綠色雞蛋,A品牌綠色雞蛋在扇形統計圖中所對應的扇形圓心角是 度;
(2)補全條形統計圖;
(3)如果該超市的另一分店在“元旦”期間共銷售這三種品牌的綠色雞蛋1500個,請你估計這個分店銷售的B種品牌的綠色雞蛋的個數?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線![]() 為一、三象限角平分線.點P關于y軸的對稱點稱為P的一次反射點,記作
為一、三象限角平分線.點P關于y軸的對稱點稱為P的一次反射點,記作![]() ;
;![]() 關于直線
關于直線![]() 的對稱點稱為點P的二次反射點,記作
的對稱點稱為點P的二次反射點,記作![]() .例如,點
.例如,點![]() 的一次反射點為
的一次反射點為![]() ,二次反射點為
,二次反射點為![]() .根據定義,回答下列問題:
.根據定義,回答下列問題:
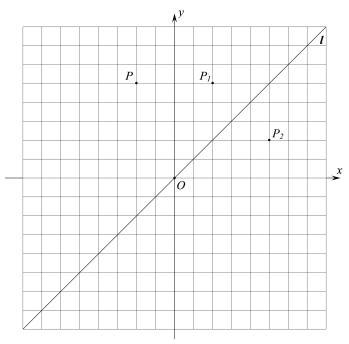
(1)點![]() 的一次反射點為________,二次反射點為__________;
的一次反射點為________,二次反射點為__________;
(2)當點A在第一象限時,點![]() ,
,![]() ,
,![]() 中可以是點A的二次反射點的是_________;
中可以是點A的二次反射點的是_________;
(3)若點A在第二象限,點![]() ,
,![]() 分別是點A的一次、二次反射點,△
分別是點A的一次、二次反射點,△![]() 為等邊三角形,求射線OA與x軸所夾銳角的度數.
為等邊三角形,求射線OA與x軸所夾銳角的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店一周內甲、乙兩種計算器每天的銷售量如下(單位:個):
類別/星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 平均數 |
甲 |
|
|
|
|
|
|
| |
乙 |
|
|
|
|
|
|
|
|
(1)將表格填寫完整.
(2)求甲種計算器本周銷售量的方差.
(3)已知乙種計算器本周銷售量的方差為![]() ,本周哪種計算器的銷售量比較穩定?說明理由.
,本周哪種計算器的銷售量比較穩定?說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道,演繹推理的過程稱為證明,證明的出發點和依據是基本事實.證明三角形全等的基本事實有:兩邊及其夾角分別相等的兩個三角形全等,兩角及其夾邊分別相等的兩個三角形全等,三邊分別相等的兩個三角形全等.
(1)請選擇利用以上基本事實和三角形內角和定理,結合下列圖形,證明:兩角分別相等且其中一組等角的對邊相等的兩個三角形全等.

(2)把三角形的三條邊和三個角統稱為三角形的六個元素.如果兩個三角形有四對對應元素相等,這兩個三角形一定全等嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=8厘米,AC=16厘米,點P從A出發,以每秒2厘米的速度向B運動,點Q從C同時出發,以每秒3厘米的速度向A運動,其中一個動點到端點時,另一個動點也相應停止運動,那么,當以A、P、Q為頂點的三角形與△ABC相似時,運動時間是多少?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com