
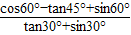
 .
.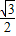 ,tan30°=
,tan30°=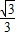 代入進行計算即可得解;
代入進行計算即可得解; ,tan45°=1,sin60°=
,tan45°=1,sin60°=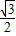 ,tan30°=
,tan30°=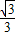 ,sin30°=
,sin30°= 代入進行計算即可得解;
代入進行計算即可得解;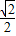 ,sin60°=
,sin60°=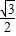 ,cos45°=
,cos45°=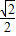 ,代入進行計算即可得解.
,代入進行計算即可得解.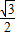 +3×
+3×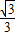
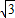 +
+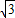
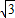 ;
;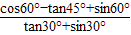
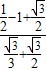
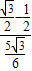
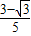 ;
;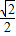 sin45°+sin60°-2cos45°
sin45°+sin60°-2cos45°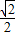 ×
×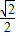 +
+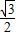 -2×
-2×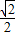
 +
+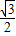 -
-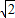 .
. ,cos30°=
,cos30°=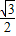 ,tan30°=
,tan30°=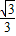 ,cot30°=
,cot30°=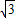 ,
,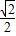 ,cos45°=
,cos45°=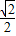 ,tan45°=1,cot45°=1,
,tan45°=1,cot45°=1,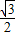 ,cos60°=
,cos60°= ,tan60°=
,tan60°=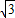 ,cot60°=
,cot60°=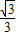 .
. 

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com