
【題目】探索研究:已知:△ABC和△CDE都是等邊三角形.
(1)如圖1,若點A、C、E在一條直線上時,我們可以得到結論:線段AD與BE的數量關系為: ,線段AD與BE所成的銳角度數為 °;
(2)如圖2,當點A、C、E不在一條直線上時,請證明(1)中的結論仍然成立;
靈活運用:
如圖3,某廣場是一個四邊形區域ABCD,現測得:AB=60m,BC=80m,且∠ABC=30°,∠DAC=∠DCA=60°,試求水池兩旁B、D兩點之間的距離.

【答案】(1)AD=BE,60;(2)證明見解析;(3)水池兩旁B、D兩點之間的距離為100m.
【解析】
試題(1)根據等邊三角形的性質可得AC=BC,CD=CE,∠ACB=∠DCE=60°,然后求出∠ACD=∠BCE,再利用“邊角邊”證明△ACD和△BCE全等,根據全等三角形對應邊相等可得AD=BE,根據全等三角形對應角相等可得∠ADC=∠BEC,然后根據三角形的一個外角等于與它不相鄰的兩個內角的和求出∠DPE=∠DCE;(2)證明△ACD≌△BCE(SAS),得到AD=BE,∠DAC=∠EBC,根據∠BPA=180°-∠ABP-∠BAP=180°-∠ABC-∠BAC,即可解答.(3)如圖3,以AB為邊在△ABC外側作等邊△ABE,連接CE,由(2)可得:BD=CE,證明△EBC是直角三角形,利用勾股定理求出CE的長度,即可解答.
試題解析:(1)∵△ABC和△CDE都是等邊三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BCE,
在△ACD和△BCE中,
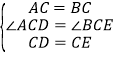 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠ADC=∠BEC,
由三角形的外角性質,∠DPE=∠PEA+∠DAC,∠DCE=∠ADC+∠DAC,
∴∠DPE=∠DCE=60°;
故答案為:相等,60;
(2)∵△ABC和△CDE都是等邊三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE,
在△ACD和△BCE中,
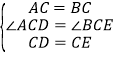 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠DAC=∠EBC,
∴∠BPA=180°﹣∠ABP﹣∠BAP=180°﹣∠ABC﹣∠BAC=60°
(3)如圖3,以AB為邊在△ABC外側作等邊△ABE,連接CE.
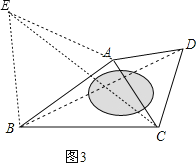
由(2)可得:BD=CE
∴∠EBC=60°+30°=90°,
∴△EBC是直角三角形
∵EB=60m BC=80m,
∴CE=![]() =100(m).
=100(m).
∴水池兩旁B、D兩點之間的距離為100m.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】已知2輛A型車和1輛B型車載滿貨物一次可運貨10噸.用1輛A型車和2輛B型車載滿貨物一次可運貨11噸.某物流公司現有31噸貨物,計劃同時租用A型車a輛和B型車b輛,一次運完,且每輛車都滿載貨物.根據以上信息解答下列問題:
(1)1輛A型車和1輛B型車載滿貨物一次分別可運貨物多少噸?
(2)請幫助物流公司設計租車方案
(3)若A型車每輛車租金每次100元,B型車每輛車租金每次120元.請選出最省錢的租車方案,并求出最少的租車費.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,P點從點A開始以2厘米/秒的速度沿A→B→C的方向移動,點Q從點C開始以1厘米/秒的速度沿C→A→B的方向移動,在直角三角形ABC中,∠A=90°,若AB=16厘米,AC=12厘米,BC=20厘米,如果P、Q同時出發,用t(秒)表示移動時間,那么:
(1)如圖1,若P在線段AB上運動,Q在線段CA上運動,試求出t為何值時,QA=AP
(2)如圖2,點Q在CA上運動,試求出t為何值時,三角形QAB的面積等于三角形ABC面積的![]() ;
;
(3)如圖3,當P點到達C點時,P、Q兩點都停止運動,試求當t為何值時,線段AQ的長度等于線段BP的長的![]()

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,與CD相交于點F,H是BC邊的中點,連結DH、BE與相交于點G,以下結論中正確的結論有( )
(1)△ABC是等腰三角形;(2)BF=AC;(3)BH:BD:BC=1:![]() :
:![]() ;(4)GE2+CE2=BG2.
;(4)GE2+CE2=BG2.
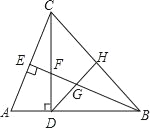
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“母親節”前夕,我市某校學生積極參與“關愛貧困母親”的活動,他們購進了一批單價為20元的“孝文化衫”在課余時間進行義賣,并將所得利潤捐給貧困母親.在義賣的過程中發現“這種文化衫每天的銷售件數y(件)與銷售單價x(元)滿足一次函數關系:y=﹣3x+108(20<x<36)”.如果義賣這種文化衫每天的利潤為p(元),那么銷售單價定為多少元時,每天獲得的利潤最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB⊥BC于點B,DC⊥BC于點C,DE平分∠ADC交BC于點E,點F為線段CD延長線上一點,∠BAF=∠EDF.
(1)求證:∠DAF=∠F;
(2)在不添加任何輔助線的情況下,請直接寫出所有與∠CED互余的角.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】寒假將近,某學校將組織七年級部分同學去亞布力參加“冰雪冬令營”.學校提前給所去學生預定房間,如果在所預定的房間里每間住![]() 人,則有
人,則有![]() 人無法安排;每間住
人無法安排;每間住![]() 人,則空出
人,則空出![]() 張床.
張床.
(1)本次參加“冰雪冬令營”的學生總數為多少人?
(2)冬令營結束時,學校準備給這些同學每人送一個售價為![]() 元的
元的![]() 或
或![]() 種紀念品,但實際購買時發現,
種紀念品,但實際購買時發現,![]() 、
、![]() 兩種商品的售價都有變動,
兩種商品的售價都有變動,![]() 種商品打八折出售,
種商品打八折出售,![]() 種商品的價錢比原售價提高了
種商品的價錢比原售價提高了![]() ,若實際購買
,若實際購買![]() 種商品費用比購買
種商品費用比購買![]() 種商品費用的
種商品費用的![]() 倍多
倍多![]() 元,那么此次活動中學校購買
元,那么此次活動中學校購買![]() 種商品多少個?
種商品多少個?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點![]() 在線段
在線段![]() 上.點
上.點![]() 從點
從點![]() 出發向點
出發向點![]() 運動,速度為2cm/s;同時,點
運動,速度為2cm/s;同時,點![]() 也從點
也從點![]() 出發用1s到達
出發用1s到達![]() 處,并在
處,并在![]() 處停留2s,然后按原速度向點
處停留2s,然后按原速度向點![]() 運動,速度為4cm/s.最終,點
運動,速度為4cm/s.最終,點![]() 比點
比點![]() 早1s到達
早1s到達![]() 處.設點
處.設點![]() 運動的時間為
運動的時間為![]() s.
s.
(1)線段![]() 的長為 cm;當
的長為 cm;當![]() =3s時,
=3s時,![]() 兩點之間的距離為 cm;
兩點之間的距離為 cm;
(2)求線段![]() 的長;
的長;
(3)從![]() 兩點同時出發至點
兩點同時出發至點![]() 到達點
到達點![]() 處的這段時間內,
處的這段時間內,![]() 為何值時,
為何值時,![]() 兩點相距1 cm?
兩點相距1 cm?
![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com