
【題目】如圖:在數軸上A點表示數a,B點示數b,C點表示數c,b是最小的正整數,且a,b滿足![]() +(c-7)2=0.
+(c-7)2=0.
(1) a= ,b= ,c= .
(2) 若將數軸折疊,使得A點與C點重合,則點B與數 表示的點重合.
(3) 點A,B,C開始在數軸上運動,若點A以每秒1個單位長度的速度向左運動,同時,點B和點C分別以每秒2個單位長度和4個單位長度的速度向右運動,假設t秒鐘過后,若點A與點B之間的距離表示為AB,點A與點C之間的距離表示為AC,點B與點C之間的距離表示為BC.則AB= ,AC= ,BC= .(用含t的代數式表示)
(4) 請問:3BC-2AB的值是否隨著時間t的變化而改變? 若變化,請說明理由;若不變,請求其值.
![]()
【答案】(1) a= -2,b=1,c=7;(2) 4;(3) AB=3t + 3,AC=5t + 9,BC=2t + 6;(4) 不變,始終為12.
【解析】試題分析:(1)利用|a+2|+(c-7)2=0,得a+2=0,c-7=0,解得a,c的值,由b是最小的正整數,可得b=1;
(2)先求出對稱點,即可得出結果;
(3)由 3BC-2AB=3(2t+6)-2(3t+3)求解即可.
試題解析:(1)∵|a+2|+(c-7)2=0,
∴a+2=0,c-7=0,
解得a=-2,c=7,
∵b是最小的正整數,
∴b=1;
(2)(7+2)÷2=4.5,
對稱點為7-4.5=2.5,2.5+(2.5-1)=4;
(3)AB=t+2t+3=3t+3,AC=t+4t+9=5t+9,BC=2t+6;
(4)不變.
3BC-2AB=3(2t+6)-2(3t+3)=12.


科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,∠DAB=60°,點E、F分別在CD、AB的延長線上,且AE=AD,CF=CB.
(1)求證:四邊形AFCE是平行四邊形;
(2)若去掉已知條件的“∠DAB=60°”,上述的結論還成立嗎?若成立,請寫出證明過程;若不成立,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
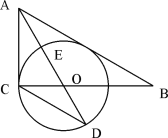
【題目】如圖,在Rt△ABC中,∠ACB=90,AO是△ABC的角平分線。以O為圓心,OC為半徑作⊙O。
(1)(3分)求證:AB是⊙O的切線。
(2)(3分)已知AO交⊙O于點E,延長AO交⊙O于點D, tanD=![]() ,求
,求![]() 的值。
的值。
(3)(4分)在(2)的條件下,設⊙O的半徑為3,求AB的長。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校九年級(1)班所有學生參加2016年初中畢業生升學體育測試,根據測試評分標準,將他們的成績進行統計后分為A、B、C、D四等,并繪制成如圖所示的條形統計圖和扇形統計圖(未完成),請結合圖中所給信息解答下列問題:
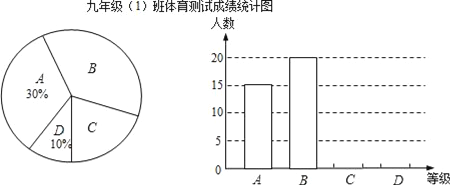
(1)九年級(1)班參加體育測試的學生有____人;
(2)將條形統計圖補充完整;
(3)在扇形統計圖中,等級B部分所占的百分比是____,等級C對應的圓心角的度數為____;
(4)若該校九年級學生共有850人參加體育測試,估計達到A級和B級的學生共有
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com