
已知:等邊![]() 的邊長為
的邊長為![]() .
.
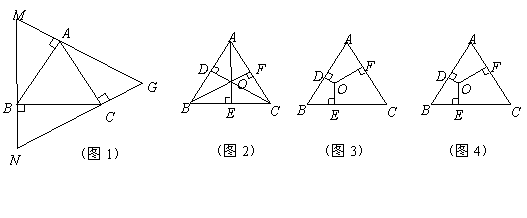
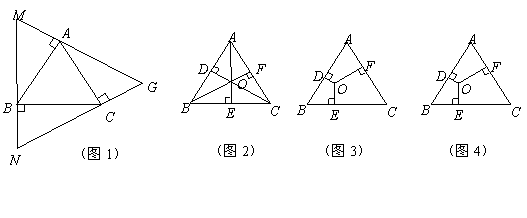
探究(1):如圖1,過等邊![]() 的頂點
的頂點![]() 依次作
依次作![]() 的垂線圍成
的垂線圍成![]() 求證:
求證:![]() 是等邊三角形且
是等邊三角形且![]() ;
;
探究(2):在等邊![]() 內取一點
內取一點![]() ,過點
,過點![]() 分別作
分別作![]() 垂足分別為點
垂足分別為點![]()
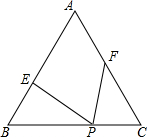
①如圖2,若點![]() 是
是![]() 的重心,我們可利用三角形面積公式及等邊三角形性質得到兩個正確結論(不必證明):結論1.
的重心,我們可利用三角形面積公式及等邊三角形性質得到兩個正確結論(不必證明):結論1.![]() ;結論2.
;結論2.![]() ;
;
②如圖3,若點![]() 是等邊
是等邊![]() 內任意一點,則上述結論
內任意一點,則上述結論![]() 是否仍然成立?如果成立,請給予證明;如果不成立,請說明理由.
是否仍然成立?如果成立,請給予證明;如果不成立,請說明理由.
 |
 各地期末復習特訓卷系列答案
各地期末復習特訓卷系列答案 小博士期末闖關100分系列答案
小博士期末闖關100分系列答案科目:初中數學 來源: 題型:
 (2013•海門市一模)已知,等邊△ABC邊長為6,P為BC邊上一點,且BP=4,點E、F分別在邊AB、AC上,且∠EPF=60°,設BE=x,CF=y.
(2013•海門市一模)已知,等邊△ABC邊長為6,P為BC邊上一點,且BP=4,點E、F分別在邊AB、AC上,且∠EPF=60°,設BE=x,CF=y.| 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 ,點
,點 在
在 正半軸上,且
正半軸上,且 .動點
.動點 在線段
在線段 上從點
上從點 向點
向點 以每秒
以每秒 個單位的速度運動,設運動時間為秒.點M、N在
個單位的速度運動,設運動時間為秒.點M、N在 軸上,且
軸上,且 是等邊三角形.
是等邊三角形. 的邊長(用的代數式表示),并求出當等邊
的邊長(用的代數式表示),并求出當等邊 的頂點
的頂點 運動到與原點
運動到與原點 重合時的值;
重合時的值; 的中點
的中點 ,以
,以 為邊在
為邊在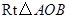 內部作如圖2所示的矩形
內部作如圖2所示的矩形 ,點
,點 在線段
在線段 上.設等邊
上.設等邊 和矩形
和矩形 重疊部分的面積為
重疊部分的面積為 ,請求出當
,請求出當 秒時,
秒時, 與的函數關系式,并求出
與的函數關系式,并求出 的最大值.
的最大值.



查看答案和解析>>
科目:初中數學 來源: 題型:
已知:等邊![]() 的邊長為
的邊長為![]() .
.
探究(1):如圖1,過等邊![]() 的頂點
的頂點![]() 依次作
依次作![]() 的垂線圍成
的垂線圍成![]() 求證:
求證:![]() 是等邊三角形且
是等邊三角形且![]() ;
;
探究(2):在等邊![]() 內取一點
內取一點![]() ,過點
,過點![]() 分別作
分別作![]() 垂足分別為點
垂足分別為點![]()
(2)如圖2,若點![]() 是
是![]() 的重心,我們可利用三角形面積公式及等邊三角形性質得到兩個正確結論(不必證明):
的重心,我們可利用三角形面積公式及等邊三角形性質得到兩個正確結論(不必證明):
① 結論1.![]() ;
;
② 結論2.![]() ;
;
(3)如圖3,若點![]() 是等邊
是等邊![]() 內任意一點,則上述結論
內任意一點,則上述結論![]() 是否仍然成立?如果成立,請給予證明;如果不成立,請說明理由.
是否仍然成立?如果成立,請給予證明;如果不成立,請說明理由.
 |
查看答案和解析>>
科目:初中數學 來源: 題型:
已知:等邊![]() 的邊長為
的邊長為![]() .
.
探究(1):如圖1,過等邊![]() 的頂點
的頂點![]() 依次作
依次作![]() 的垂線圍成
的垂線圍成![]() 求證:
求證:![]() 是等邊三角形且
是等邊三角形且![]() ;
;
探究(2):在等邊![]() 內取一點
內取一點![]() ,過點
,過點![]() 分別作
分別作![]() 垂足分別為點
垂足分別為點![]()
①如圖2,若點![]() 是
是![]() 的重心,我們可利用三角形面積公式及等邊三角形性質得到兩個正確結論(不必證明):結論1.
的重心,我們可利用三角形面積公式及等邊三角形性質得到兩個正確結論(不必證明):結論1.![]() ;結論2.
;結論2.![]() ;
;
②如圖3,若點![]() 是等邊
是等邊![]() 內任意一點,則上述結論
內任意一點,則上述結論![]() 是否仍然成立?如果成立,請給予證明;如果不成立,請說明理由.
是否仍然成立?如果成立,請給予證明;如果不成立,請說明理由.
 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com