已知:某函數的自變量x>0時,其相應的函數值y>1.
(1)請寫出一個滿足條件的一次函數的解析式;
(2)當函數的解析式為y=(m+4)x2-2(m+4)x+5-m時,求m的取值范圍;
(3)過動點C(0,n)作直線l⊥y軸,點O為坐標原點.
①當直線l與(2)中的拋物線只有一個公共點時,求n的取值范圍;
②當直線l與(2)中的拋物線相交于A、B兩點時,是否存在實數n,使得△AOB的面積為定值?如果存在,求出n的值;如果不存在,說明理由.
【答案】
分析:(1)只要y=kx+b中只要k>0則y隨x的增大而增大,因而只要b≥1即可滿足條件;
(2)當m=-4時,是一個常數函數,當m≠-4時,首先表示出二次函數的頂點坐標,根據y>0,可以得到拋物線開口向上,且頂點的縱坐標大于1,即可求得m的范圍;
(3)①直線l與(2)的拋物線只有一個公共點,則頂點的縱坐標是n,即可得到m、n的關系,根據m的范圍即可求得n的范圍;
②把y=n代入拋物線的解析式,對于任意的m的值,得到的式子恒成立,據此即可求得n的值,則根據A、B的坐標的關系即可作判斷.
解答:解:(1)y=x+2(答案不唯一);
(2)當m=-4時,y=9;
當m≠-4時,y=(m+4)x
2-2(m+4)+5-m的頂點坐標是:(1,-2m+1),
根據題意得:
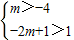
,
解得:-4<m<0.
綜上所述,m的范圍是:-4<m<0;
(3)①∵直線l與(2)的拋物線只有一個公共點,
∴n=-2m+1
∵-4<m<0,
∴n的范圍是:1<n<9;
②結論:存在實數n,使得△AOB的面積為定值.
理由:n=(m+4)x
2-2(m+4)x+5-m,
整理,得:(x
2-2x-1)m+(4x
2-8x+5-n)=0,
∵對于任意的m的值,上式恒成立,
∴

,
解得:n=9.
∴當n=9時,對于任意的m的值,二次函數y=(m+4)x
2-2(m+4)x+5-m的圖象都通過點(1-

,9)和點(1+

,9),即△AOB的底AB=2

,高是9,因此面積是定值.
點評:本題主要考查了二次函數解析式的確定、函數圖象交點的求法等知識點,還涉及到的知識點有拋物線的頂點公式和三角形的面積求法.

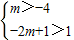 ,
, ,
, ,9)和點(1+
,9)和點(1+ ,9),即△AOB的底AB=2
,9),即△AOB的底AB=2 ,高是9,因此面積是定值.
,高是9,因此面積是定值.
