
【題目】已知x軸上有點A(1,0),點B在y軸上,點C(m,0)為x軸上一動點且m<﹣1,連接AB,BC,tan∠ABO= ![]() ,以線段BC為直徑作⊙M交直線AB于點D,過點B作直線l∥AC,過A,B,C三點的拋物線為y=ax2+bx+c,直線l與拋物線和⊙M的另一個交點分別是E,F.
,以線段BC為直徑作⊙M交直線AB于點D,過點B作直線l∥AC,過A,B,C三點的拋物線為y=ax2+bx+c,直線l與拋物線和⊙M的另一個交點分別是E,F.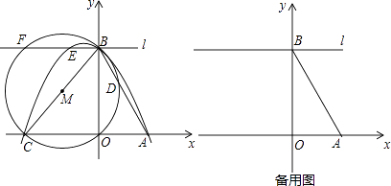
(1)求B點坐標;
(2)用含m的式子表示拋物線的對稱軸;
(3)線段EF的長是否為定值?如果是,求出EF的長;如果不是,說明理由.
(4)是否存在點C(m,0),使得BD= ![]() AB?若存在,求出此時m的值;若不存在,說明理由.
AB?若存在,求出此時m的值;若不存在,說明理由.
【答案】
(1)
解:∵tan∠ABO= ![]() ,且A(1,0),
,且A(1,0),
∴OB=2,即:點B的坐標為(0,2)
(2)
解:點C(m,0),A(1,0),B(0,2)在拋物線y=ax2+bx+c上,
∴ 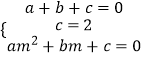
解之得:b=﹣ ![]() ,a=
,a= ![]() ,
,
∴x=﹣ ![]() =
= ![]() .
.
即:拋物線的對稱軸為x= ![]()
(3)
解:∵點E在拋物線y=ax2+bx+c上,又在直線y=2上,
∴2=ax2+bx+2
∴x1=0,x2=﹣ ![]()
∴E(﹣ ![]() ,2),
,2),
又∵直線l∥x軸,BC是⊙M的直徑,
∴BF∥OC,BF=OC,
∴F(m,2)
∴EF=﹣ ![]() ﹣m,
﹣m,
∵點C(m,0)為x軸上一動點且m<﹣1,
∴m的值是一個變量,
即:線段EF的長不是定值
(4)
解:如下圖所示:連接CD
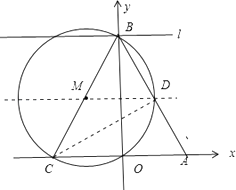
∵BCS是⊙M的直徑,
∴∠CDB=90°,
∵若BD= ![]() AB,即BD=DA
AB,即BD=DA
則易證CB=CA
∴ ![]() =1﹣m
=1﹣m
解之得m=﹣ ![]() ,
,
即:存在一點C(﹣ ![]() ,0),使得BD=
,0),使得BD= ![]() AB
AB
【解析】(1)根據正切函數的定義及點A的坐標求解;(2)因為點C、A、B在拋物線上,故代入其坐標列方程組求解即可;(3)點E(x,y)既在拋物線y=ax2+bx+2上,又在直線y=2上,所以有2=ax2+bx+2,由此可知E(﹣ ![]() ,2),又因為直線l∥x軸,BC是⊙M的直徑,由圓的對稱性可知BF∥OC且BF=OC,所以F(m,2),由此可分析EF長;(4)連接CD,因為BC為圓的直徑,所以∠BDC=90°,若BD=
,2),又因為直線l∥x軸,BC是⊙M的直徑,由圓的對稱性可知BF∥OC且BF=OC,所以F(m,2),由此可分析EF長;(4)連接CD,因為BC為圓的直徑,所以∠BDC=90°,若BD= ![]() AB,可證明CA=CB,由此可求得符合題意的點C(﹣
AB,可證明CA=CB,由此可求得符合題意的點C(﹣ ![]() ,0).
,0).


 永乾教育寒假作業快樂假期延邊人民出版社系列答案
永乾教育寒假作業快樂假期延邊人民出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c與x軸的負半軸交于點A,B(點A在點B的右邊),與y軸的正半軸交于點C,且OA=OC=1,則下列關系中正確的是( ) 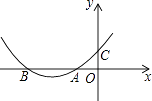
A.a+b=1
B.b<2a
C.a﹣b=﹣1
D.ac<0
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商品公司為指導某種應季商品的生產和銷售,在對歷年市場行情和生產情況進行調查基礎上,對今年這種商品的市場售價和生產成本進行了預測并提供了兩個方面的信息:如圖(1)(2). 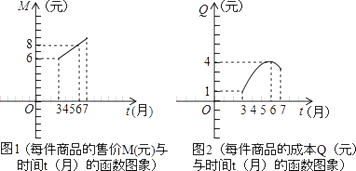
注:兩圖中的每個實心黑點所對應的縱坐標分別指相應月份一件商品的售價和成本,生產成本6月份最高;圖(1)的圖象是線段,圖(2)的圖象是拋物線.
(1)在3月份出售這種商品,一件商品的利潤是多少?
(2)設t月份出售這種商品,一件商品的成本Q(元),求Q關于t的函數解析式.
(3)設t月份出售這種商品,一件商品的利潤W(元),求W關于t的函數解析式.
(4)問哪個月出售這種商品,一件商品的利潤最大?簡單說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知線段AB
(1)請用尺規按下列要求作圖:
①延長線段AB到C,使BC=AB,
②延長線段BA到D,使AD=AC(不寫畫法,當要保留畫圖痕跡)
(2)請直接回答線段BD與線段AC長度之間的大小關系
(3)如果AB=2cm,請求出線段BD和CD的長度.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,菱形ABCD的頂點A的坐標為(2,0),點B的坐標為(0,1),點C在第一象限,對角線BD與x軸平行.直線y=x+4與x軸、y軸分別交于點E,F.將菱形ABCD沿x軸向左平移k個單位,當點C落在△EOF的內部時(不包括三角形的邊),k的值可能是( )

A.2 B.3 C.4 D.5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一家商店因換季將某種服裝打折銷售,每件服裝如果按標價的4折出售將虧40元,而按標價8折出售將賺40元.問:
(1)每件服裝的標價是多少元?
(2)每件服裝的成本是多少元?
(3)為了保證不虧損,最多可以打幾折?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料:小華遇到這樣一個問題:
已知:如圖1,在△ABC中,三邊的長分別為AB= ![]() ,AC=
,AC= ![]() ,BC=2,求∠A的正切值.
,BC=2,求∠A的正切值.
小華是這樣解決問題的:
如圖2所示,先在一個正方形網格(每個小正方形的邊長均為1)中畫出格點△ABC(△ABC三個頂點都在小正方形的頂點處),然后在這個正方形網格中再畫一個和△ABC相似的格點△DEF,從而使問題得解.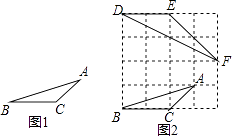
(1)如圖2,△DEF中與∠A相等的角為 , ∠A的正切值為 .
(2)參考小華的方法請解決問題:若△LMN的三邊分別為LM=2,MN=2 ![]() ,LN=2
,LN=2 ![]() ,求∠N的正切值.
,求∠N的正切值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】材料1:反射定律
當入射光線AO照射到平面鏡上時,將遵循平面鏡反射定律,即反射角(∠BOM)的大小等于入射角(∠AOM)的大小,顯然,這兩個角的余角也相等,其中法線(OM)與平面鏡垂直,并且滿足入射光線、反射光線(OB)與法線在同一個平面.
材料2:平行逃逸角
對于某定角∠AOB=α(0°<α<90°),點P為邊OB上一點,從點P發出一光線PQ(射線),其角度為∠BPQ=β(0°<β<90°),當光線PQ接觸到邊OA和OB時會遵循反射定律發生反射,當光線PQ經過n次反射后與邊OA或OB平行時,稱角為定角α的n階平行逃逸角,特別地,當光線PQ直接與OA平行時,稱角β為定角α的零階平行逃逸角.
(1)已知∠AOB=α=20°,
①如圖1,若PQ∥OA,則∠BPQ= °,即該角為α的零階平行逃逸角;
②如圖2,經過一次反射后的光線P1Q∥OB,此時的∠BPP1為α的平行逃逸角,求∠BPP1的大小;
③若經過兩次反射后的光線與OA平行,請補全圖形,并直接寫出α的二階平行逃逸角為 °;
(2)根據(1)的結論,歸納猜想對于任意角α(0°<α<90°),其n(n為自然數)階平行逃逸角β= (用含n和a的代數式表示).

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com