
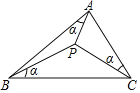
【題目】如圖,若△ABC內一點P,滿足∠PAB=∠PBC=∠PCA=α,則稱點P為△ABC的布洛卡點.通過研究一些特殊三角形中的布洛卡點,得到如下兩個結論:
①若∠BAC=90°,則必有∠APC=90°;②若AB=AC,則必有∠APB=∠BPC.
對于這兩個結論,下列說法正確的是( )
A.①對,②錯B.①錯,②對C.①,②均錯D.①,②均對
科目:初中數學 來源: 題型:
【題目】為發展學生的核心素養,培養學生的綜合能力,某學校計劃開設四門選修課:樂器、舞蹈、繪畫、書法,學校采取隨機抽樣的方法進行問卷調查![]() 每個被調查的學生必須選擇而且只能選擇其中一門
每個被調查的學生必須選擇而且只能選擇其中一門![]() 對調查結果進行整理,繪制成如下兩幅不完整的統計圖
對調查結果進行整理,繪制成如下兩幅不完整的統計圖![]() 請結合圖中所給信息解答下列問題:
請結合圖中所給信息解答下列問題:


![]() 本次調查的學生共有______人,在扇形統計圖中,m的值是______.
本次調查的學生共有______人,在扇形統計圖中,m的值是______.
![]() 分別求出參加調查的學生中選擇繪畫和書法的人數,并將條形統計圖補充完整.
分別求出參加調查的學生中選擇繪畫和書法的人數,并將條形統計圖補充完整.
![]() 該校共有學生2000人,估計該校約有多少人選修樂器課程?
該校共有學生2000人,估計該校約有多少人選修樂器課程?
查看答案和解析>>
科目:初中數學 來源: 題型:
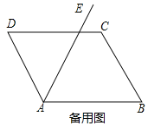
【題目】如圖1,在□ABCD中,![]() ,
,![]() ,
,![]() ,射線AE平分
,射線AE平分![]() 動點P以
動點P以![]() 的速度沿AD向終點D運動,過點P作
的速度沿AD向終點D運動,過點P作![]() 交AE于點Q,過點P作
交AE于點Q,過點P作![]() ,過點Q作
,過點Q作![]() ,交PM于點
,交PM于點![]() 設點P的運動時間為
設點P的運動時間為![]() ,四邊形APMQ與四邊形ABCD重疊部分面積為
,四邊形APMQ與四邊形ABCD重疊部分面積為![]()


![]() ______
______![]() 用含t的代數式表示
用含t的代數式表示![]()
![]() 當點M落在CD上時,求t的值.
當點M落在CD上時,求t的值.
![]() 求S與t之間的函數關系式.
求S與t之間的函數關系式.
![]() 如圖2,連結AM,交PQ于點G,連結AC、BD交于點H,直接寫出t為何值時,GH與三角形ABD的一邊平行或共線.
如圖2,連結AM,交PQ于點G,連結AC、BD交于點H,直接寫出t為何值時,GH與三角形ABD的一邊平行或共線.
查看答案和解析>>
科目:初中數學 來源: 題型:
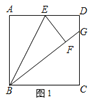
【題目】![]() 如圖
如圖![]() ,正方形
,正方形![]() 的邊長為
的邊長為![]() ,點
,點![]() 是
是![]() 邊的中點,將
邊的中點,將![]() 沿
沿![]() 翻折得到
翻折得到![]() ,延長
,延長![]() 交
交![]() 邊于點
邊于點![]() ,則
,則![]() ,求出此時
,求出此時![]() 的值;
的值;
![]() 如圖
如圖![]() ,矩形
,矩形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 是
是![]() 邊的中點,同樣將
邊的中點,同樣將![]() 沿
沿![]() 翻折得到
翻折得到![]() ,延長
,延長![]() 交
交![]() 邊于點
邊于點![]() .
.
①證明:![]() ;
;
②若點![]() 恰是
恰是![]() 邊的中點,求
邊的中點,求![]() 的值;
的值;
③若![]() 與
與![]() 相似,求
相似,求![]() 的值.
的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
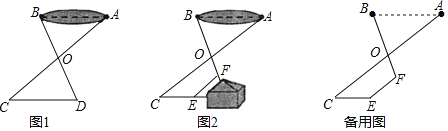
【題目】如圖1,為測量池塘寬度AB,可在池塘外的空地上取任意一點O,連接AO,BO,并分別延長至點C,D,使OC=OA,OD=OB,連接CD
(1)求證:AB=CD;
(2)如圖2,受地形條件的影響,于是采取以下措施:延長AO至點C,使OC=OA,過點C作AB的平行線CE,延長BO至點F,連接EF,測得∠CEF=140°,∠OFE=110°,CE=11m,EF=10m,請直接寫出池塘寬度AB.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】A玉米試驗田是邊長為am的正方形減去邊長為1m的蓄水池后余下部分,B玉米試驗田是邊長為(a-1)m的正方形,兩塊試驗田的玉米都收獲了500kg.
(1)哪種玉米田的單位面積產量高?
(2)高的單位面積產量是低的單位面積產量的多少倍?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】高爾夫球手基礎的高爾夫球的運動路線是一條拋物線,當球水平運動了![]() 時達到最高點.落球點比擊球點的海拔低
時達到最高點.落球點比擊球點的海拔低![]() ,水平距離為
,水平距離為![]() .
.
![]() 建立適當的坐標系,求高度
建立適當的坐標系,求高度![]() 關于水平距離
關于水平距離![]() 的二次函數式;
的二次函數式;
![]() 與擊球點相比,運動到最高點時有多高?
與擊球點相比,運動到最高點時有多高?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 是矩形
是矩形![]() 內一點,
內一點,![]() 于點
于點![]() ,
,![]() 于點
于點![]() ,
,![]() .
.

![]() 請判斷四邊形
請判斷四邊形![]() 是否是正方形?若是,寫出證明過程:若不是,說明理由;
是否是正方形?若是,寫出證明過程:若不是,說明理由;
![]() 延長
延長![]() 到點
到點![]() ,使
,使![]() ,連接
,連接![]() 交
交![]() 的延長線于點
的延長線于點![]() ,求
,求![]() 的度數.
的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com