
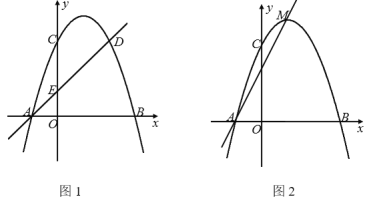
【題目】如圖1,拋物線y=ax2+bx+c與x軸交于A(-1,0),B(3,0)兩點,與y軸交于點C. 點D(2,3)在該拋物線上,直線AD與y軸相交于點E,點F是直線AD上方的拋物線上的動點.
(1)求該拋物線對應的二次函數關系式;
(2)當點F到直線AD距離最大時,求點F的坐標;
(3)如圖2,點M是拋物線的頂點,點P的坐標為(0,n),點Q是坐標平面內一點,以A,M,P,Q為頂點的四邊形是AM為邊的矩形.①求n的值;②若點T和點Q關于AM所在直線對稱,求點T的坐標.
【答案】(1)y=-x2+2x+3;(2)F(![]() ,
,![]() );(3)n=
);(3)n=![]() ,T(0,-
,T(0,-![]() )或n=-
)或n=-![]() ,T(0,
,T(0,![]() ).
).
【解析】
(1)用待定系數法求解即可;
(2)作FH⊥AD,過點F作FM⊥x軸,交AD與M,易知當S△FAD最大時,點F到直線AD距離FH最大,求出直線AD的解析式,設F(t,-t2+2t+3),M(t,t+1),表示出△FAD的面積,然后利用二次函數的性質求解即可;
(3)分AP為對角線和AM為對角線兩種情況求解即可.
解:(1)∵拋物線x軸相交于點A(-1,0),B(3,0),
∴設該拋物線對應的二次函數關系式為y=a(x+1)(x-3),
∵點D(2,3)在拋物線上,
∴3=a×(2+1) ×(2-3),
∴3=-3a,
∴a=-1,
∴y=-(x+1)(x-3),
即y=-x2+2x+3;
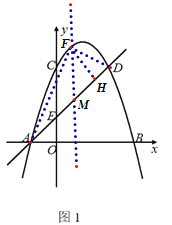
(2)如圖1,作FH⊥AD,過點F作FM⊥x軸,交AD與M,易知當S△FAD最大時,點F到直線AD距離FH最大,
設直線AD為y=kx+b,
∵A(-1,0),D(2,3),
∴![]() ,
,
∴![]() ,
,
∴直線AD為y=x+1.
設點F的橫坐標為t,則F(t,-t2+2t+3),M(t,t+1),
∵S△FAD= S△AMF+ S△DMF=![]() MF(Dx-Ax)
MF(Dx-Ax)
= ![]() ×3(-t2+2t+3-t-1)=
×3(-t2+2t+3-t-1)=![]() ×3(-t2+t+2)
×3(-t2+t+2)
=-![]() (t-
(t-![]() )2+
)2+![]() ,
,
∴即當t=![]() 時,S△FAD最大,
時,S△FAD最大,
∵當x=![]() 時,y=-(
時,y=-(![]() )2+2×
)2+2×![]() +3=
+3=![]() ,
,
∴F(![]() ,
,![]() );
);
(3)∵y=-x2+2x+3=-(x-1)2+4,
∴頂點M(1,4).
當AP為對角線時,如圖2,
設拋物線對稱軸交x軸于點R,作PS⊥MR,
∵∠PMS+∠AMR=90°, ∠MAR+∠AMR=90°,
∴∠PMA=∠MAR,
∵∠PSM=∠ARM=90°,
∴△PMS∽△MAR,
∴![]() ,
,
∴![]() ,
,
∴MS=![]() ,
,
∴OP=RS=4+![]() =
=![]() ,
,
∴n=![]() ;
;
延長QA交y軸于T,
∵PM∥AQ,
∴∠MPO=∠OAM,
∵∠MPS+∠MPO=90°, ∠OAT+∠OAM=90°,
∴∠MPS=∠OAT.
又∵PS=OA=1,∠PSM=∠AOT=90°,
∴△PSM≌△AOT,
∴AT=PM=AQ,OT=MS=![]() .
.
∵AM⊥AQ,
∴T和Q關于AM對稱,
∴T(0,-![]() );
);
當AQ為對角線時,如圖3,
過A作SR⊥x軸,作PS⊥SR于S,作MR⊥SR于R,
∵∠RAM+∠SAP=90°, ∠SAP+∠SPA=90°,
∴∠RAM=∠SPA,
∵∠PSA=∠ARM=90°,
∴△PSA∽△ARM,
∴![]() ,
,
∴![]() ,
,
∴AS=![]() ,
,
∴OP=![]() ,
,
∴n=-![]() ;
;
延長QM交y軸于T,
∵QM∥AP,
∴∠APT=∠MTP,
∵∠OAP+∠APT=90°, ∠GMT+∠MTP=90°,
∴∠OAP=∠GMT.
又∵GM=OA=1,∠AOP=∠MGT=90°,
∴△OAP≌△GMT,
∴MT=AP=MQ,GT=OP=![]() .
.
∵AM⊥TQ,
∴T和Q關于AM對稱,
∵OT=4+![]() =
=![]() ,
,
∴T(0,![]() ).
).
綜上可知,n=![]() ,T(0,-
,T(0,-![]() )或n=-
)或n=-![]() ,T(0,
,T(0,![]() ).
).


 習題精選系列答案
習題精選系列答案科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,過⊙O外一點P作⊙O的兩條切線PC,PD,切點分別為C,D,連接OP,CD.
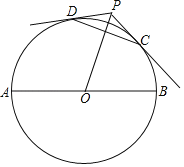
(1)求證:OP⊥CD;
(2)連接AD,BC,若∠DAB=50°,∠CBA=70°,OA=2,求OP的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
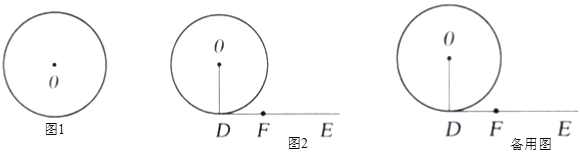
【題目】(1)①如圖1,請用直尺(不帶刻度)和圓規作出![]() 的內接正三角形
的內接正三角形![]() (按要求作圖,不要求寫作法,但要保留作圖痕跡).
(按要求作圖,不要求寫作法,但要保留作圖痕跡).
②若![]() 的內接正三角形
的內接正三角形![]() 邊長為6,求
邊長為6,求![]() 的半徑;
的半徑;
(2)如圖2,![]() 的半徑就是(1)中所求半徑的值.點
的半徑就是(1)中所求半徑的值.點![]() 在
在![]() 上,
上,![]() 是
是![]() 的切線,點
的切線,點![]() 在射線
在射線![]() 上,且
上,且![]() ,點
,點![]() 從點
從點![]() 出發,以每秒1個單位的速度沿射線
出發,以每秒1個單位的速度沿射線![]() 方向移動,點
方向移動,點![]() 是
是![]() 上的點(不與點
上的點(不與點![]() 重合),
重合),![]() 是
是![]() 的切線.設點
的切線.設點![]() 運動的時間為
運動的時間為![]() (秒),當
(秒),當![]() 為何值時,
為何值時,![]() 是直角三角形,請你求出滿足條件的所有
是直角三角形,請你求出滿足條件的所有![]() 值.
值.
查看答案和解析>>
科目:初中數學 來源: 題型:
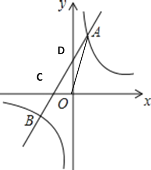
【題目】如圖,已知反比例函數![]() 的圖像與一次函數
的圖像與一次函數![]() 的圖象相交于點A(1,4)和點B(m,-2).
的圖象相交于點A(1,4)和點B(m,-2).
(1)求反比例函數和一次函數的解析式;
(2)求ΔAOC的面積;
(3)直接寫出![]() 時的x的取值范圍 (只寫答案)
時的x的取值范圍 (只寫答案)
查看答案和解析>>
科目:初中數學 來源: 題型:
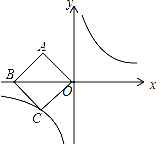
【題目】如圖,在平面直角坐標系中,正方形ABCO的對角線BO在x軸上,若正方形ABCO的邊長為4![]() ,點B在x負半軸上,反比例函數的圖象經過C點.
,點B在x負半軸上,反比例函數的圖象經過C點.
(1)求該反比例函數的解析式;
(2)若點P是反比例函數上的一點,且△PBO的面積恰好等于正方形ABCO的面積,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的口袋里有標號為![]() 的五個小球,除數字不同外,小球沒有任何區別,摸球前先攪拌均勻,每次摸一個球.
的五個小球,除數字不同外,小球沒有任何區別,摸球前先攪拌均勻,每次摸一個球.
(1)下列說法:
①摸一次,摸出一號球和摸出![]() 號球的概率相同;
號球的概率相同;
②有放回的連續摸![]() 次,則一定摸出
次,則一定摸出![]() 號球兩次;
號球兩次;
③有放回的連續摸![]() 次,則摸出四個球標號數字之和可能是
次,則摸出四個球標號數字之和可能是![]() .
.
其中正確的序號是
(2)若從袋中不放回地摸兩次,求兩球標號數字是一奇一偶的概率,(用列表法或樹狀圖)
查看答案和解析>>
科目:初中數學 來源: 題型:
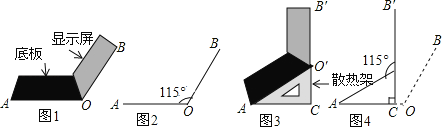
【題目】將筆記本電腦放置在水平桌面上,顯示屏OB與底板OA夾角為115°(如圖1),側面示意圖為圖2;使用時為了散熱,在底板下面墊入散熱架O′AC后,電腦轉到AO′B′的位置(如圖3),側面示意圖為圖4,已知OA=0B=20cm,B′O′⊥OA,垂足為C.
(1)求點O′的高度O′C;(精確到0.1cm)
(2)顯示屏的頂部B′比原來升高了多少?(精確到0.1cm)
(3)如圖4,要使顯示屏O′B′與原來的位置OB平行,顯示屏O′B′應繞點O′按順時針方向旋轉多少度?
參考數據:(sin65°=0.906,cos65°=0.423,tan65°=2.146.cot65°=0.446)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com