
已知△ABC是等腰直角三角形,∠A = 90°,D是腰AC上的一個動點,過C作CE垂直于BD或BD的延長線,垂足為E,如圖.
(1)若BD是AC的中線,求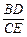 的值;
的值;
(2)若BD是∠ABC的角平分線,求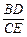 的值;
的值;
(3)結合(1)、(2),試推斷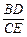 的取值范圍(直接寫出結論,不必證明),并探究
的取值范圍(直接寫出結論,不必證明),并探究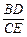 的
的
值能小于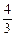 嗎?若能,求出滿足條件的D點的位置;若不能,說明理由
嗎?若能,求出滿足條件的D點的位置;若不能,說明理由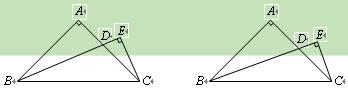
解法1 設AB =" AC" = 1,CD = x,則0<x<1,BC =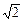 ,AD = 1-x.
,AD = 1-x.
在Rt△ABD中,BD2 = AB2 + AD2 =" 1" +(1-x)2 = x2-2x + 2.
由已知可得 Rt△ABD∽Rt△ECD,
∴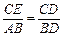 ,即
,即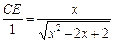 ,從而
,從而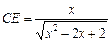 ,
,
∴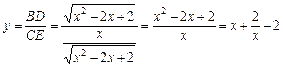 ,0<x<1,
,0<x<1,
(1)若BD是AC的中線,則CD =" AD" =" x" =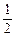 ,得
,得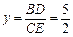 .
.
(2)若BD是∠ABC的角平分線,則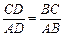 ,得
,得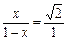 ,解得
,解得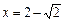 ,
,
∴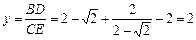 .
.
(3)若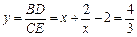 ,則有 3x2-10x + 6 = 0,解得
,則有 3x2-10x + 6 = 0,解得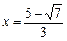 ∈(0,1),
∈(0,1),
∴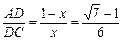 ,表明隨著點D從A向C移動時,BD逐漸增大,而CE逐漸減小,的值則隨著D從A向C移動而逐漸增大.
,表明隨著點D從A向C移動時,BD逐漸增大,而CE逐漸減小,的值則隨著D從A向C移動而逐漸增大.
解法2 設AB =" AC" = 1,∠ABD = a,則 BC =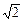 ,∠CBE = 45°-a.
,∠CBE = 45°-a.
在Rt△ABD中,有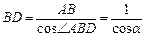 ;
;
在Rt△BCE中,有 CE =" BC·" sin∠CBE =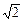 sin(45°-a).[來源:Z+xx+k.Com]
sin(45°-a).[來源:Z+xx+k.Com]
因此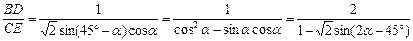 .下略……
.下略……
解法3 (1)∵∠A =∠E = 90°,∠ADB =∠CDE,∴△ADB∽△EDC,∴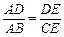 .
.
由于D是中點,且AB  = AC,知AB =" 2" AD,于是 CE =" 2" DE.
= AC,知AB =" 2" AD,于是 CE =" 2" DE.
在Rt△ADB中,BD =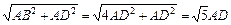 .
.
在Rt△CDE中,由 CE2 + DE2 = CD2,有 CE2 +
CE2 + CE2 = CD2,于是
CE2 = CD2,于是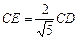 .
.
而 AD = CD,所以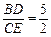 .
.
(2)如圖,延長CE、BA相交于點F.∵BE是∠ABC的平分線,且BE⊥CF,∴△CBE≌△FBE,得 CE = EF,于是CF =" 2" CE.又∠ABD +∠ADB =∠CDE +∠FCA = 90°,且∠ADB =∠CDE,
∴∠ABD =∠FCA,進而有△ABD≌△ACF,得 BD =" 2" CE,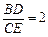 .
.
(3)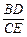 的值的取值范圍為
的值的取值范圍為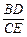 ≥1.下略……
≥1.下略……
解析


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
 學習過三角函數,我們知道在直角三角形中,一個銳角的大小與兩條邊長的比值相互唯一確定,因此邊長與角的大小之間可以相互轉化.類似的,也可以在等腰三角形中建立邊角之間的聯系,我們定義:等腰三角形中底邊與腰的比叫做頂角的正對(sad).如圖,在△ABC中,AB=AC,頂角A的正對記作sadA,這時sad A=
學習過三角函數,我們知道在直角三角形中,一個銳角的大小與兩條邊長的比值相互唯一確定,因此邊長與角的大小之間可以相互轉化.類似的,也可以在等腰三角形中建立邊角之間的聯系,我們定義:等腰三角形中底邊與腰的比叫做頂角的正對(sad).如圖,在△ABC中,AB=AC,頂角A的正對記作sadA,這時sad A=| 1 |
| 2 |
| 2 |
| 2 |
| 3 |
| 3 |
| 3 |
| 5 |
2-2
|
2-2
|
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 學習過三角函數,我們知道在直角三角形中,一個銳角的大小與兩條邊長的比值相互唯一確定,因此邊長與角的大小之間可以相互轉化.類似的,也可以在等腰三角形中建立邊角之間的聯系,我們定義:等腰三角形中底邊與腰的比叫做頂角的正對(sad).如圖,在△ABC中,AB=AC,頂角A的正對記作sadA,這時sad A=
學習過三角函數,我們知道在直角三角形中,一個銳角的大小與兩條邊長的比值相互唯一確定,因此邊長與角的大小之間可以相互轉化.類似的,也可以在等腰三角形中建立邊角之間的聯系,我們定義:等腰三角形中底邊與腰的比叫做頂角的正對(sad).如圖,在△ABC中,AB=AC,頂角A的正對記作sadA,這時sad A= .容易知道一個角的大小與這個角的正對值也是相互唯一確定的.
.容易知道一個角的大小與這個角的正對值也是相互唯一確定的.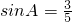 ,其中A為銳角,試求sadA的值;
,其中A為銳角,試求sadA的值;查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com