在Rt△ABC中,AB=BC=4,∠B=90°,將一直角三角板的直角頂點放在斜邊AC的中點P處,將三角板繞點P旋轉,三角板的兩直角邊分別與邊AB、BC或其延長線上交于D、E兩點(假設三角板的兩直角邊足夠長),如圖(1)、圖(2)表示三角板旋轉過程中的兩種情形.
(1)直角三角板繞點P旋轉過程中,當BE=______
【答案】
分析:(1)根據△PEC是等腰三角形,分類進行討論即可;
(2)連接BP,首先根據題干條件證明出∠BPD=∠CPE,然后證明△DPB≌△EPC,于是證明出PD=PE;
(3)過M分別作AB、BC的垂線,垂足分別為G、H,首先根據角之間的關系求出∠GMD=∠HME,進而證明出△MGD∽△MHE,根據相似三角形對應邊成比例,得到
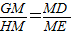
,再求出GM、HM關于m、n的表達式,三式結合求出MD、ME之間的比例關系.
解答:(1)解:當BE=0時,即點B和點E重合,故可知△PEC是等腰三角形,
當BE=2時,即E是BC的中點,可得△PEC是等腰三角形
由題干條件知PC=2
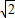
,當CP=CE時△PEC是等腰三角形,BE=4-2
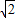
;
當E在BC的延長線上時,CE=CP,△PEC是等腰三角形,BE=4+2
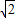
;
故答案為0、2或4±2
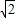
.
(2)證明:連接BP.
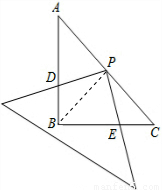
∵AB=BC 且∠ABC=90°,
∴∠C=45°,
又∵P是AC中點,
∴BP⊥AC,BP=PC 且∠ABP=∠CBP=45°,
∴∠CPE+∠EPB=90°,
∵DP⊥PE,
∴∠BPD+∠EPB=90°,
∴∠BPD=∠CPE,
在△DPB和△EPC中
∵
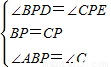
,
∴△DPB≌△EPC,
∴PD=PE,
(3)解:MD、ME的數量關系是:
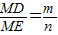
,
理由如下:
過M分別作AB、BC的垂線,垂足分別為G、H.
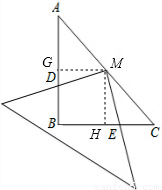
由作圖知,∠MGA=∠MGB=∠MHB=∠MHE=90°
又∵∠B=90°,
∴∠GMH=90°,
∴∠GMD+∠DMH=90°,
∵∠DMH+∠HME=90°,
∴∠GMD=∠HME
∴△MGD∽△MHE,
∴
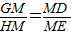
①,
∵
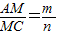
,
∴
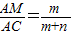
,
∵∠MGA=∠B=90°,
∴GM∥BC,
∴
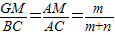
即
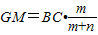
②
同理
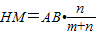
,
∵AB=BC,
∴
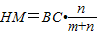
③
②③代入①得
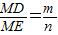
.
點評:本題主要考查相似綜合題得知識點,解答本題的關鍵是熟練運用相似三角形的判定與性質定理,此題難度較大.

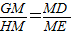 ,再求出GM、HM關于m、n的表達式,三式結合求出MD、ME之間的比例關系.
,再求出GM、HM關于m、n的表達式,三式結合求出MD、ME之間的比例關系.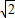 ,當CP=CE時△PEC是等腰三角形,BE=4-2
,當CP=CE時△PEC是等腰三角形,BE=4-2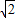 ;
; 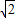 ;
;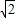 .
. 
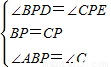 ,
,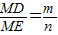 ,
,
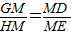 ①,
①,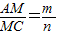 ,
,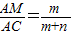 ,
,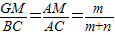 即
即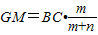 ②
②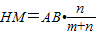 ,
,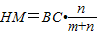 ③
③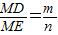 .
.

 長江作業本同步練習冊系列答案
長江作業本同步練習冊系列答案 小天才課時作業系列答案
小天才課時作業系列答案 一課四練系列答案
一課四練系列答案 黃岡小狀元滿分沖刺微測驗系列答案
黃岡小狀元滿分沖刺微測驗系列答案