Question

（2013年四川資陽12分）如圖，四邊形ABCD是平行四邊形，過點A、C、D作拋物線y=ax²+bx+c（a≠0），與x軸的另一交點為E，連結CE，點A、B、D的坐標分別為（﹣2，0）、（3，0）、（0，4）．

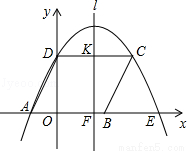
（1）求拋物線的解析式；

（2）已知拋物線的對稱軸l交x軸于點F，交線段CD于點K，點M、N分別是直線l和x軸上的動點，連結MN，當線段MN恰好被BC垂直平分時，求點N的坐標；

（3）在滿足（2）的條件下，過點M作一條直線，使之將四邊形AECD的面積分為3：4的兩部分，求出該直線的解析式．

 

Answer 1

【答案】

解：（1）∵點A、B、D的坐標分別為（﹣2，0）、（3，0）、（0，4），且四邊形ABCD是平行四邊形，

∴AB=CD=5。∴點C的坐標為（5，4）。

∵拋物線y=ax²+bx+c（a≠0）過點A、C、D，

∴，解得]。

∴拋物線的解析式為。

（2）連接BD交對稱軸于G，

      在Rt△OBD中，易求BD=5，

∴CD=BD，則∠DCB=∠DBC。

又∵∠DCB=∠CBE，∴∠DBC=∠CBE。

過G作GN⊥BC于H，交x軸于N，易證GH=HN，

∴點G與點M重合。

∴直線BD的解析式。 

根據拋物線可知對稱軸方程為x=，

則點M的坐標為（，），即GF= MF=，BF=。

∴。

又∵MN被BC垂直平分，∴BM=BN=。∴BN=OB+BN=3+。

∴點N的坐標為（，0）。

（3）過點M作直線交x軸于點P₁，

易求四邊形AECD的面積為28，四邊形ABCD的面積為20，

由“四邊形AECD的面積分為3：4”可知直線P₁M必與線段CD相交，

設交點為Q₁，四邊形AP₁Q₁D的面積為S₁，四邊形P₁ECQ₁的面積為S₂，點P₁的坐標為（a，0），則S₂=12。

若點P在對稱軸的左側，則P₁F=﹣a，P₁E=7﹣a，

由△MKQ₁∽△MFP₁，得。∴Q₁K=5P₁F=5（﹣a）。

∴CQ₁=﹣5（﹣a）=5a﹣10。

∴。∴。

根據P₁（，0），M（，）可求直線P₁M的解析式為。

若點P在對稱軸的右側，同理可得直線P₂M的解析式為。

綜上所述，該直線的解析式為或。

【解析】（1）根據平行四邊形的性質可求點C的坐標，由待定系數法即可求出拋物線的解析式。

（2）連接BD交對稱軸于G，過G作GN⊥BC于H，交x軸于N，根據待定系數法即可求出直線BD的解析式，根據拋物線對稱軸公式可求對稱軸，由此即可求出點N的坐標。

（3）過點M作直線交x軸于點P₁，分點P在對稱軸的左側，點P在對稱軸的右側，兩種情況討論即可求出直線的解析式。

考點：二次函數綜合題，雙動點問題，4待定系數法的應用，曲線上點的坐標與方程的關系，平行四邊形的性質，二次函數的性質，勾股定理，相似三角形的判定和性質，分類思想的應用。