
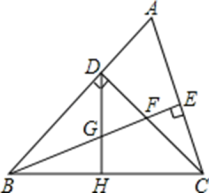
【題目】已知:如圖,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,與CD相交于點F,H是BC邊的中點,連結DH與BE相交于點G.
(1)求證:BF=AC;
(2)求證:CE=![]() BF.
BF.
【答案】(1)詳見解析;(2)詳見解析.
【解析】
(1)利用ASA判定Rt△DFB≌Rt△DAC,從而得出BF=AC.
(2)利用ASA判定Rt△BEA≌Rt△BEC,得出CE=AE=![]() AC,再由BF=AC,利用等量代換即可得結論.
AC,再由BF=AC,利用等量代換即可得結論.
(1)∵CD⊥AB,∠ABC=45°,
∴△BCD是等腰直角三角形,
∴BD=CD,
∵CD⊥AB,BE⊥AC,
∴∠BDC=∠CDA=90°,∠BEC=∠BEA=90°,
∴∠DBF=90°-∠BFD,∠DCA=90°-∠EFC,
又∵∠BFD=∠EFC,
∴∠DBF=∠DCA.
在Rt△DFB和Rt△DAC中,
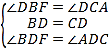 ,
,
∴Rt△DFB≌Rt△DAC(ASA),
∴BF=AC;
(2)∵BE平分∠ABC,
∴∠ABE=∠CBE.
在Rt△BEA和Rt△BEC中
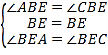 ,
,
∴Rt△BEA≌Rt△BEC(ASA),
∴CE=AE,
∵CE+AE=AC,
∴CE=![]() AC,
AC,
又由(1)知BF=AC,
∴CE=![]() BF.
BF.


科目:初中數學 來源: 題型:
【題目】有一個n位自然數![]() 能被x0整除,依次輪換個位數字得到的新數
能被x0整除,依次輪換個位數字得到的新數![]() 能被x0+1整除,再依次輪換個位數字得到的新數
能被x0+1整除,再依次輪換個位數字得到的新數![]() 能被x0+2整除,按此規律輪換后,
能被x0+2整除,按此規律輪換后,![]() 能被x0+3整除,…,
能被x0+3整除,…,![]() 能被x0+n﹣1整除,則稱這個n位數
能被x0+n﹣1整除,則稱這個n位數![]() 是x0的一個“輪換數”.
是x0的一個“輪換數”.
例如:60能被5整除,06能被6整除,則稱兩位數60是5的一個“輪換數”;
再如:324能被2整除,243能被3整除,432能被4整除,則稱三位數324是2個一個“輪換數”.
(1)若一個兩位自然數的個位數字是十位數字的2倍,求證這個兩位自然數一定是“輪換數”.
(2)若三位自然數![]() 是3的一個“輪換數”,其中a=2,求這個三位自然數
是3的一個“輪換數”,其中a=2,求這個三位自然數![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,AB=BC=2,∠ABC=120°,將△ABC繞著點B順時針旋轉角a(0°<a<90°)得到△A1BC;A1B交AC于點E,A1C1分別交AC、BC于D、F兩點.
(1)如圖1,觀察并猜想,在旋轉過程中,線段BE與BF有怎樣的數量關系?并證明你的結論.
(2)如圖2,當a=30°時,試判斷四邊形BC1DA的形狀,并證明.
(3)在(2)的條件下,求線段DE的長度.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,點O為原點,平行于x軸的直線與拋物線L:y=ax2相交于A,B兩點(點B在第一象限),點C在AB的延長線上.
(1)已知a=1,點B的縱坐標為2.如圖1,向右平移拋物線L使該拋物線過點B,與AB的延長線交于點C,AC的長為__.
(2)如圖2,若BC=AB,過O,B,C三點的拋物線L3,頂點為P,開口向下,對應函數的二次項系數為a3,![]() =__.
=__.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形紙片ABCD中,AB=6,BC=8.把△BCD沿對角線BD折疊,使點C落在C′處,BC′交AD于點G;E、F分別是C′D和BD上的點,線段EF交AD于點H,把△FDE沿EF折疊,使點D落在D′處,點D′恰好與點A重合.

(1)求證:△ABG≌△C′DG;
(2)求tan∠ABG的值;
(3)求EF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB∥CD,∠ABK的角平分線BE的反向延長線和∠DCK的角平分線CF的反向延長線交于點H,∠K﹣∠H=27°,則∠K=( )

A. 76° B. 78° C. 80° D. 82°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某校一幢教學大樓的頂部豎有一塊“傳承文明,啟智求真”的宣傳牌CD.小明在山坡的坡腳A處測得宣傳牌底部D的仰角為60°,沿山坡向上走到B處測得宣傳牌頂部C的仰角為45°.已知山坡AB的坡度i=1:,AB=10米,AE=15米,求這塊宣傳牌CD的高度.(測角器的高度忽略不計,結果精確到0.1米.參考數據:≈1.414,≈1.732)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某地為了鼓勵居民節約用水,決定實行兩級收費制,即每月用水量不超過14噸(含14噸)時,每噸按政府補貼優惠價收費;每月超過14噸時,超過部分每噸按市場調節價收費,小英家1月份用水20噸,交水費29元;2月份用水18噸,交水費24元.
(1)求每噸水的政府補貼優惠價和市場調節價分別是多少?
(2)小英家3月份用水24噸,她家應交水費多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠MON=45°,P為∠MON內一點,A為OM上一點,B為ON上一點,當![]() PAB的周長取最小值時,∠APB的度數為( )
PAB的周長取最小值時,∠APB的度數為( )

A.80°B.90°C.110°D.120°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com